题目内容
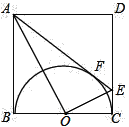
【题目】如图,在正方形ABCD中,以BC为直径的正方形内,作半圆O,AE切半圆于点F交CD于E
(1) 求证:AO⊥EO
(2) 连接DF,求tan∠FDE的值
【答案】(1)证明见解析;
(2)tan∠FDE的值是![]()
【解析】试题分析:(1)、根据切线的性质得出∠BAO=∠FAO,∠CEO=∠FEO,根据四边形的性质得出∠BAE+∠CEA=180°,从而说明∠DAF+∠OEF=90°,得出垂直;(2)、设OB=OC=2,则AB=4,根据△AOB和△OEC全等得出CE=EF=1,DE=3,AE=5,过点F作FG⊥DE于G,则FG∥AD,根据平行线截线段成比例得出FG、EG和DG的长度,最后根据三角函数的计算法则得出答案.
试题解析:(1) ∵∠ABC=∠DCB=90° ∴AD、CD均为半圆的切线
连接OF ∵AE切半圆于E ∴∠BAO=∠FAO,∠CEO=∠FEO ∵∠BAE+∠CEA=180°
∴∠DAF+∠OEF=90° ∴∠AOE=90° ∴AO⊥EO
(2) 设OB=OC=2,则AB=4 ∵Rt△AOB∽Rt△OEC ∴CE=EF=1,DE=3,AE=5
过点F作FG⊥DE于G ∴FG∥AD
∴![]() 即
即![]() ∴FG=
∴FG=![]() ,EG=
,EG=![]() ,DG=
,DG=![]() ∴tan∠FDE=
∴tan∠FDE=![]()

练习册系列答案
相关题目