题目内容
【题目】已知:如图所示,∠ABD和∠BDC的平分线交于E,BE交CD于点F,∠1+∠2=90°. 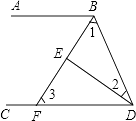
(1)求证:AB∥CD;
(2)试探究∠2与∠3的数量关系.
【答案】
(1)证明:∵BE、DE平分∠ABD、∠BDC,
∴∠1= ![]() ∠ABD,∠2=
∠ABD,∠2= ![]() ∠BDC;
∠BDC;
∵∠1+∠2=90°,
∴∠ABD+∠BDC=180°;
∴AB∥CD;(同旁内角互补,两直线平行)
(2)解:∵DE平分∠BDC,
∴∠2=∠FDE;
∵∠1+∠2=90°,
∴∠BED=∠DEF=90°;
∴∠3+∠FDE=90°;
∴∠2+∠3=90°.
【解析】(1)已知BE、DE平分∠ABD、∠BDC,且∠1+∠2=90°,可得∠ABD+∠BDC=180°,根据同旁内角互补,可得两直线平行.(2)已知∠1+∠2=90°,即∠BED=90°;那么∠3+∠FDE=90°,将等角代换,即可得出∠3与∠2的数量关系.
【考点精析】关于本题考查的角的平分线和平行线的判定,需要了解从一个角的顶点引出的一条射线,把这个角分成两个相等的角,这条射线叫做这个角的平分线;同位角相等,两直线平行;内错角相等,两直线平行;同旁内角互补,两直线平行才能得出正确答案.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
【题目】学校准备设计一款女生校服,对全校女生喜欢的颜色进行了问卷调查,统计如下表所示:
颜色 | 黄色 | 绿色 | 白色 | 紫色 | 红色 |
学生人数 | 100 | 180 | 220 | 80 | 750 |
学校决定采用红色,可用来解释这一现象的统计知识是( )
A. 平均 B. 中位数 C. 众数 D. 方差