题目内容
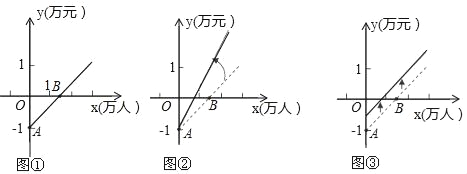
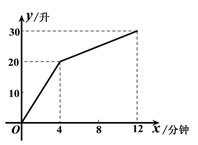
【题目】一个装有进水管和出水管的容器,从某时刻开始的4分钟内只进水不出水,在随后的8分钟内既进水又出水,接着关闭进水管直到容器内的水放完.假设每分钟的进水量和出水量是两个常数,容器内的水量y(单位:升)与时间x(单位:分钟)之间的部分关系如图象所示.求从关闭进水管起需要多少分钟该容器内的水恰好放完.
【答案】从关闭进水管起需要8分钟该容器内的水恰好放完.
【解析】
先根据函数图象求出进水管的进水量和出水管的出水量,由工程问题的数量关系就可以求出结论.
解:由函数图象,得:
进水管每分钟的进水量为:20÷4=5(升).
设出水管每分钟的出水量为 m升,由函数图象,得:
20+(5-m)×(12-4)=30.
解得:m=![]()
∴30÷![]() =8(分钟).
=8(分钟).
即从关闭进水管起需要8分钟该容器内的水恰好放完.

练习册系列答案
相关题目
【题目】如图,伞不论张开还是收紧,伞柄AP始终平分同一平面内两条伞架所成的角∠BAC,当伞收紧时,结点D与点M重合,且点A、E、D在同一条直线上,已知部分伞架的长度如下:单位:cm
伞架 | DE | DF | AE | AF | AB | AC |
长度 | 36 | 36 | 36 | 36 | 86 | 86 |
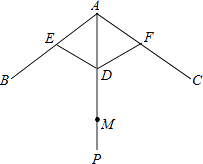
(1)求AM的长.
(2)当∠BAC=104°时,求AD的长(精确到1cm). 备用数据:sin52°=0.788,cos52°=0.6157,tan52°=1.2799.