��Ŀ����
����Ŀ���±��Dz���ѧУ����һ��ۻۡ��ϴ�����ѧ����ѧ����10����ѧ���ɼ�����λ���֣���
�ۻ� | 116 | 124 | 130 | 126 | 121 | 127 | 126 | 122 | 125 | 123 |
�ϴ� | 122 | 124 | 125 | 128 | 119 | 120 | 121 | 128 | 114 | 119 |
�ش��������⣺
��1���ֱ�����ۻۺʹϴϳɼ���ƽ������
��2���ֱ����ۻۺʹϴ��������ݵķ��
��3�����ݣ�1����2������Ϊѡ˭�μ�ȫ����ѧ���������ʣ���˵�����ɣ�
��4�����ڳ������ࡢ��������ͳ����İ���ѧ�ɼ���Ա�����ѧУ�����ɻۻۺʹϴϷֱ�μ����������ѧҵ�ศ�����������ѧ���ֱ��ڳ�������ͳ�������ĸ��ʣ�
���𰸡�
��1���⣺�ۻ۵�ƽ������=125+ ![]() ����9��1+5+1+6+2+1��3+0��2��=125���֣���
����9��1+5+1+6+2+1��3+0��2��=125���֣���
�ϴϵ�ƽ������=125+ ![]() ����3��1+0+3��6��5+6+3��11��6��=123���֣�
����3��1+0+3��6��5+6+3��11��6��=123���֣�
��2���⣺�ۻ۳ɼ��ķ��� S2= ![]() [92+12+52+12+42+22+12+32+02+22]=14.2��
[92+12+52+12+42+22+12+32+02+22]=14.2��
�ϴϳɼ��ķ���S2= ![]() [12+12+22+52+42+32+82+52+92+42]=24.2
[12+12+22+52+42+32+82+52+92+42]=24.2
��3���⣺���ݣ�1����֪�ۻ۵�ƽ���ɼ�Ҫ���ڴϴϣ����ݣ�2����֪�ۻ۵ķ���С�ڴϴϵķ����Ϊ����ԽСԽ�ȶ������Իۻ۵ijɼ��ȴϴϵ��ȶ������ѡ�ۻ۲μ�ȫ����ѧ����������һЩ��
��4���⣺����״ͼΪ��
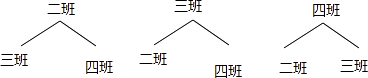
����6�ֵȿ��ܵĽ��������������ѧ���ֱ��ڳ�������ͳ�������Ľ����Ϊ2��
��������ѧ���ֱ��ڳ�������ͳ�������ĸ���= ![]() =
= ![]()
�����������⿼�����б�������״ͼ����ͨ���б�������״ͼ��չʾ���еȿ��ܵĽ�����n���ٴ���ѡ�������¼�A��B�Ľ����Ŀm��Ȼ����ݸ��ʹ�ʽ����¼�A��B�ĸ��ʣ�Ҳ������ƽ�����ļ��㷽���ͷ���ļ��㣮��1���ѻۻۺʹϴϵijɼ�����ȥ125��Ȼ��������ǵ�ƽ���ɼ�����2�����ݷ��ʽ�����������ݵķ����3������ƽ�����Ĵ�С�ͷ������������жϣ���4������״ͼչʾ����6�ֵȿ��ܵĽ���������ҳ�����ѧ���ֱ��ڳ�������ͳ�������Ľ������Ȼ����ݸ��ʹ�ʽ���㣮
�����㾫�������ڱ��⿼����б�������״ͼ��������ƽ��������Ҫ�˽һ������Ҫ�����������������ʱ�����б����Ͳ������ˣ�Ϊ�˲��ز�©���г����п��ܵĽ����ͨ��������״ͼ������ʣ����������ܷ���=ƽ����������ؼ��Ǹ�����֪����ȷ���������Լ��������Ӧ���ܷ������ܵó���ȷ�𰸣�

 ��ʦ�㲦��ϵ�д�
��ʦ�㲦��ϵ�д� Ӣ�żƻ���ĩ����ϵ�д�
Ӣ�żƻ���ĩ����ϵ�д�








