Question

【题目】如图，AB是⊙O的直径，点P在BA的延长线上，弦CD⊥AB，垂足为E，且PC2=PEPO．

（1）求证：PC是⊙O的切线．
（2）若OE：EA=1：2，PA=6，求⊙O的半径．

Answer 1

【答案】
（1）证明：连结OC，如图，

∵CD⊥AB，

∴∠PEC=90°，

∵PC2=PEPO，

∴PC：PO=PE：PC，

而∠CPE=∠OPC，

∴△PCE∽△POC，

∴∠PEC=∠PCO=90°，

∴OC⊥PC，

∴PC是⊙O的切线

（2）解：设OE=x，则EA=2x，OA=OC=3x，

∵∠COE=∠POC，∠OEC=∠OCP，

∴△OCE∽△OPC，

∴OC：OP=OE：OC，即3x：OP=x：3x，解得OP=9x，

∴3x+6=9x，解得x=1，

∴OC=3，

即⊙O的半径为3．

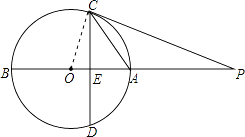
【解析】本题考查了相似三角形的判定与性质：在判定两个三角形相似时，应注意利用图形中已有的公共角、公共边等隐含条件，以充分发挥基本图形的作用．也考查了切线的判定方法．（1）连结OC，如图，由PC2=PEPO和公共角可判断△PCE∽△POC，则∠PEC=∠PCO=90°，然后根据切线的判定定理可判断PC是⊙O的切线；（2）设OE=x，则EA=2x，OA=OC=3x，证明△OCE∽△OPC，利用相似比可表示出OP，则可列方程3x+6=9x，然后解出x即可得到⊙O的半径．
【考点精析】根据题目的已知条件，利用垂径定理和切线的判定定理的相关知识可以得到问题的答案，需要掌握垂径定理：平分弦（不是直径）的直径垂直于弦，并且平分弦所对的两条弧；切线的判定方法：经过半径外端并且垂直于这条半径的直线是圆的切线．