Question

如图，在矩形中，，，点是边上的动点（点不与点，点重合），过点作直线，交边于点，再把沿着动直线对折，点的对应点是点，设的长度为，与矩形重叠部分的面积为．

（1）求的度数；

（2）当取何值时，点落在矩形的边上？

（3）①求与之间的函数关系式；

②当取何值时，重叠部分的面积等于矩形面积的？

Answer 1

解：（1）如图，四边形是矩形，．

又，，，

，．

，．

，．

（2）如图1，由轴对称的性质可知，，

，．

由（1）知，，

，．

，，．

在中，根据题意得：，

解这个方程得：．

（3）①当点在矩形的内部或边上时，

，

，当时，

当在矩形的外部时（如图2），，

      

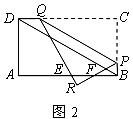
在中，，

，

又，，

在中，

，．

，

，

当时，．

综上所述，与之间的函数解析式是：．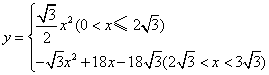

②矩形面积，当时，函数随自变量的增大而增大，所以的最大值是，而矩形面积的的值，

而，所以，当时，的值不可能是矩形面积的；

当时，根据题意，得：

，解这个方程，得，因为，

所以不合题意，舍去．

所以．

综上所述，当时，与矩形重叠部分的面积等于矩形面积的．