题目内容
【题目】在五边形ADBCE中,∠ADB=∠AEC=90°,∠DAB=∠EAC,M、N、O分别为AC、AB、BC的中点.
(1)求证:△EMO≌△OND;
(2)若AB=AC,且∠BAC=40°,当∠DAB等于多少时,四边形ADOE是菱形,并证明.

【答案】(1)证明见解析(2)当∠DAB等于35°时,四边形ADOE是菱形
【解析】试题分析:(1)根据直角三角形斜边中线等于斜边一半得:DN=![]() AB,由中位线定理得:OM=
AB,由中位线定理得:OM=![]() AB,则OM=DN,同理得:ON=ME,再根据外角定理和已知证明其夹角相等,则两三角形全等;
AB,则OM=DN,同理得:ON=ME,再根据外角定理和已知证明其夹角相等,则两三角形全等;
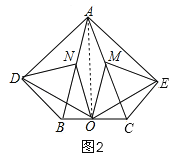
(2)连接AO,当∠DAB等于35°时,四边形ADOE是菱形,如图2,设∠DAB=x°,则∠BND=2x°,易证得OD=OE,AD=AE,因此只要AD=OD,四边形ADOE就是菱形;即∠DAO=∠AOD,列关于x的方程解出即可.
试题解析:证明:(1)∵∠ADB=90°,N是AB的中点,∴DN=![]() AB=AN,∴∠ADN=∠BAD,∵O是AB的中点,M是AC的中点,∴OM是△ABC的中位线,∴OM=
AB=AN,∴∠ADN=∠BAD,∵O是AB的中点,M是AC的中点,∴OM是△ABC的中位线,∴OM=![]() AB,OM∥AB,∴∠OMC=∠BAC,同理得:∠BNO=∠BAC,∴∠BNO=∠OMC,∵DN=
AB,OM∥AB,∴∠OMC=∠BAC,同理得:∠BNO=∠BAC,∴∠BNO=∠OMC,∵DN=![]() AB,OM=
AB,OM=![]() AB,∴DN=OM,同理得:ME=ON,∵∠BND=∠ADN+∠BAD,∠CME=∠CAE+∠AEM,∴∠BND=2∠BAD,∠CME=2∠CAE,∵∠BAD=∠CAE,∴∠BND=∠CME,∴∠BND+∠BNO=∠CME+∠OMC,即∠DNO=∠EMO,∴△EMO≌△OND;
AB,∴DN=OM,同理得:ME=ON,∵∠BND=∠ADN+∠BAD,∠CME=∠CAE+∠AEM,∴∠BND=2∠BAD,∠CME=2∠CAE,∵∠BAD=∠CAE,∴∠BND=∠CME,∴∠BND+∠BNO=∠CME+∠OMC,即∠DNO=∠EMO,∴△EMO≌△OND;
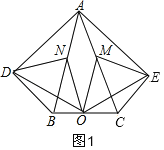
(2)当∠DAB等于35°时,四边形ADOE是菱形,理由是:
如图2,连接AO,设∠DAB=x°,则∠BND=2x°,∵AB=AC,O是BC的中点,∴AO平分∠BAC,AO⊥BC,∵∠BAC=40°,∴∠BAO=20°,在Rt△ABO中,N是AB的中点,∴ON=![]() AB=AN,∴∠BAO=∠AON=20°,∴∠BNO=40°,由(1)得:ON=
AB=AN,∴∠BAO=∠AON=20°,∴∠BNO=40°,由(1)得:ON=![]() AC,DN=
AC,DN=![]() AB,∴ON=DN,∴∠NDO=∠NOD=
AB,∴ON=DN,∴∠NDO=∠NOD=![]() (180°-∠DNO)=90°﹣
(180°-∠DNO)=90°﹣![]() (2x°+40°)=70°﹣x°,∵∠ADB=∠AEC=90°,∠BAD=∠CAE,AB=AC,∴△ADB≌△AEC,∴AD=AE,由(1)得:△EMO≌△OND,∴OD=OE,∴当AD=OD时,四边形ADOE是菱形,即∠DAO=∠AOD,x+20=70﹣x+20,x=35,∴当∠DAB等于35°时,四边形ADOE是菱形.
(2x°+40°)=70°﹣x°,∵∠ADB=∠AEC=90°,∠BAD=∠CAE,AB=AC,∴△ADB≌△AEC,∴AD=AE,由(1)得:△EMO≌△OND,∴OD=OE,∴当AD=OD时,四边形ADOE是菱形,即∠DAO=∠AOD,x+20=70﹣x+20,x=35,∴当∠DAB等于35°时,四边形ADOE是菱形.

 阅读快车系列答案
阅读快车系列答案

