Question

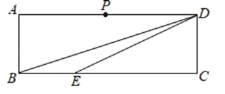
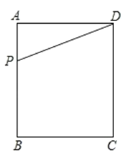
【题目】如图，在矩形中，，，点是边上的一动点，连结．

（1）若将沿折叠，点落在矩形的对角线上点处，试求的长；

（2）点运动到某一时刻，过点作直线交于点，将与分别沿与折叠，点与点分别落在点，处，若，，三点恰好在同一直线上，且试求此时的长；

（3）当点运动到边的中点处时，过点作直线交于点，将与分别沿与折叠，点与点重合于点处，连结，请求出的长．

Answer 1

【答案】（1）的长为或；（2）的长为1或3；（3）．

【解析】

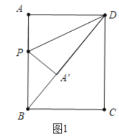
（1）分两种情形：①当点A落在对角线BD上时，设AP=PA′=x，构建方程即可解决问题；②当点A落在对角线AC上时，利用相似三角形的性质构建方程即可解决问题；

（2）分两种情形分别求解即可解决问题；

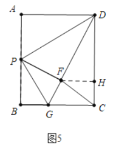
（3）如图5中，作FH⊥CD由H．想办法求出FH、CH即可解决问题；

（1）①当点落在对角线上时，设，

在，∵，，∴，

∵，∴，

在中，，解得，

∴．

②当点落在对角线上时，

由翻折性质可知：，则有，

∴，∴．

∴的长为或；

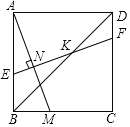
（2）①如图3中，设，则，

根据折叠的性质可知：，，

∴，∴，∴，；

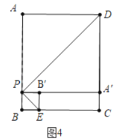
②如图4中，设，则，

根据折叠的性质可知：，，

∵，∴，

∴，∴；

综上所述，的长为1或3；

（3）如图5中，作由．

由翻折的性质可知；．，共线，

设，在中，，

解得，∴，，

∵，∴，∴，

∴，，∴，

在中，．