题目内容
【题目】已知,如图,在四边形OABC中,AB∥OC,BC⊥x轴于点C,A(1,﹣1),B(3,﹣1),动点P从点O出发,沿着x轴正方向以每秒2个单位长度的速度移动,过点P作PQ垂直于直线OA,垂足为点Q,设点P移动的时间t秒(0<t<2),△OPQ与四边形OABC重叠部分的面积为S.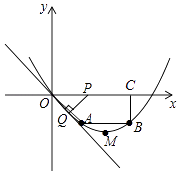
(1)求经过O、A、B三点的抛物线的解析式,并确定顶点M的坐标;
(2)用含t的代数式表示点P、点Q的坐标;
(3)求出S与t的函数关系式.
【答案】
(1)
解:设抛物线解析式为y=ax2+bx(a≠0),
把点A(1,﹣1),B(3,﹣1)代入得,
![]() ,
,
解得: 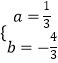 ,
,
故抛物线解析式为y= ![]() x2﹣
x2﹣ ![]() x
x
(2)
解:∵点P从点O出发速度是每秒2个单位长度,
∴OP=2t,
∴点P的坐标为(2t,0),
∵A(1,﹣1),
∴∠AOC=45°,
∴点Q到x轴、y轴的距离都是 ![]() OP=
OP= ![]() ×2t=t,
×2t=t,
∴点Q的坐标为(t,﹣t)
(3)
解:如图,点Q与点A重合时,
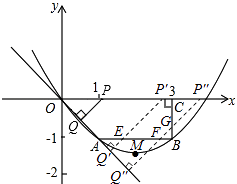
OP=1×2=2,t=2÷2=1,
点P与点C重合时,OP=3,t=3÷2=1.5,
t=2时,OP=2×2=4,PC=4﹣3=1,此时PQ经过点B,
所以,分三种情况讨论:
①0<t≤1时,重叠部分的面积等于△POQ的面积,S= ![]() ×(2t)×
×(2t)× ![]() =t2,
=t2,
②1<t≤1.5时,重叠部分的面积等于两个等腰直角三角形的面积的差,
S=S△OP′Q′﹣S△AEQ′= ![]() ×(2t)×
×(2t)× ![]() ﹣
﹣ ![]() ×(
×( ![]() t﹣
t﹣ ![]() )2=2t﹣1;
)2=2t﹣1;
③1.5<t<2时,重叠部分的面积等于梯形的面积减去一个等腰直角三角形的面积
S=S梯形OABC﹣S△BGF= ![]() ×(2+3)×1﹣
×(2+3)×1﹣ ![]() ×[1﹣(2t﹣3)]2=﹣2(t﹣2)2+
×[1﹣(2t﹣3)]2=﹣2(t﹣2)2+ ![]() ;
;
所以,S与t的关系式为S=  .
.
【解析】(1)设抛物线解析式为y=ax2+bx(a≠0),然后把点A、B的坐标代入求出a、b的值,即可得解,再把函数解析式整理成顶点式形式,然后写出顶点M的坐标;(2)根据点P的速度求出OP,即可得到点P的坐标,再根据点A的坐标求出∠AOC=45°,然后判断出△POQ是等腰直角三角形,根据等腰直角三角形的性质求出点Q的坐标即可;(3)求出点Q与点A重合时的t=1,点P与点C重合时的t=1.5,t=2时PQ经过点B,然后分①0<t≤1时,重叠部分的面积等于△POQ的面积,②1<t≤1.5时,重叠部分的面积等于两个等腰直角三角形的面积的差,③1.5<t<2时,重叠部分的面积等于梯形的面积减去一个等腰直角三角形的面积分别列式整理即可得解.
【考点精析】利用二次函数的性质对题目进行判断即可得到答案,需要熟知增减性:当a>0时,对称轴左边,y随x增大而减小;对称轴右边,y随x增大而增大;当a<0时,对称轴左边,y随x增大而增大;对称轴右边,y随x增大而减小.

【题目】某面粉加工厂加工的面粉,用每袋可装10g面粉的袋子装了200袋经过称重,质量超过标准质量10kg的用正数表示,质量低于标准质量10kg的用负数表示,结果记录如下
与标准质量的偏差(kg) | ﹣1.5 | ﹣1 | ﹣0.5 | 0 | 0.5 | 1 | 2 |
袋数(袋) | 40 | 30 | 10 | 25 | 40 | 20 | 35 |
(1)求这批面粉的总质量;
(2)如果100kg小麦加工80kg面粉,那么这批面粉是由多少千克小麦加工的?



