题目内容
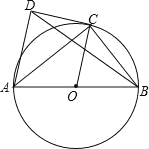
【题目】如图,AB为⊙O的直径,C为⊙O上一点,AD和过点C的切线互相垂直,垂足为D.
(1)求证:AC平分∠DAB;
(2)若sin∠ABC=![]() ,求tan∠BDC的值.
,求tan∠BDC的值.
【答案】(1)证明见解析;
(2)tan∠CDB=tan∠DBM=![]() =
=![]() =
=![]() .
.
【解析】
试题分析:(1)先证明AD∥OC,得∠DAC=∠ACO,再根据OA=OC得∠OAC=∠OCA,由此即可证明.
(2)连接BM、OC交于点N,根据sin∠ABC=sin∠BCN=![]() =
=![]() ,设BN=4k,BC=5k,则CN=3k,求出DM,BM,根据tan∠CDB=tan∠DBM=
,设BN=4k,BC=5k,则CN=3k,求出DM,BM,根据tan∠CDB=tan∠DBM=![]() 即可解决问题.
即可解决问题.
试题解析:(1)∵DC是⊙O切线,
∴OC⊥CD,∵AD⊥CD,
∴AD∥CO,
∴∠DAC=∠ACO,
∵OA=OC,
∴∠OAC=∠ACO,
∴∠DAC=∠CAO,
∴AC平分∠DAB.
(2)连接BM、OC交于点N.
∵AB是直径,
∴∠AMB=90°,∵AD∥OC,
∴∠ONB=∠AMB=90°=∠CNB,
∵OC=OB,
∴∠OCB=∠OBC,
∴sin∠ABC=sin∠BCN=![]() =
=![]() ,设BN=4k,BC=5k,则CN=3k,
,设BN=4k,BC=5k,则CN=3k,
∵∠CDM=∠DMN=∠DCN=90°,
∴四边形DMNC是矩形,
∴DM=CN=3k,MN=BN=4k,CD∥BM,
∴∠CDB=∠DBM,
∴tan∠CDB=tan∠DBM=![]() =
=![]() =
=![]() .
.


 口算题天天练系列答案
口算题天天练系列答案【题目】小林在某商店购买商品A,B共三次,只有其中一次购买时,商品A,B同时打折,其余两次均按标价购买,三次购买商品A、B的数量和费用如表所示,
购买商品A的数量/个 | 购买商品B的数量/个 | 购买总费用/元 | |
第一次购物 | 6 | 5 | 1140 |
第二次购物 | 3 | 7 | 1110 |
第三次购物 | 9 | 8 | 1062 |
(1)在这三次购物中,第几次购物打了折扣;
(2)求出商品A、B的标价;
(3)若商品A、B的折扣相同,问商店是打几折出售这两种商品的?


