题目内容
【题目】(1)任意四边形四边中点围成的四边形是__________;
(2)对角线相等的四边形四边中点围成的四边形是__________;
(3)对角线垂直的四边形四边中点围成的四边形是__________;并证明.
【答案】平行四边形菱形矩形
【解析】
(1)连接任意四边形的中点,如图,连接AC,根据三角形的中位线定理,可以证得HG=FE=![]() AC,并且HG∥EF,所以利用平行四边形的判定定理可知,该中点四边形是平行四边形.
AC,并且HG∥EF,所以利用平行四边形的判定定理可知,该中点四边形是平行四边形.
(2)在(1)的基础上,易证平行四边形GHBF的一组邻边相等,所以根据菱形的定义可知该中点四边形是菱形.
(3)在(1)的基础上,易证平行四边形GHBF中有一个角是直角,所以根据矩形的定义可知该中点四边形是矩形.
(1)如图所示,任意四边形ABCD中,E、F、G、H分别为各边的中点,求四边形EFGH的形状.
连接AC,
∵E、F、G、H分别为各边的中点,
∴HG、EF分别为△ACD与△ABC的中位线,
∴HG∥AC∥EF,HG=EF=![]() AC,
AC,
∴四边形EFGH是平行四边形;
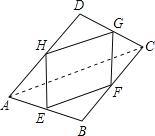
(2)如图所示,四边形ABCD的对角线AC=BD,E、F、G、H分别为各边的中点,求四边形EFGH的形状.
连接AC、BD,
∵E、F、G、H分别为各边的中点,
∴EH、GF分别为△ABD与△BCD的中位线,
∴EH∥BD∥GF,EH=GF=![]() BD,
BD,
∴四边形EFGH是平行四边形,
同理可得,HG=EF=![]() AC,
AC,
∵AC=BD,
∴EH=GF,
∴四边形EFGH是菱形;

(3)如图所示,四边形ABCD的对角线AC⊥BD,E、F、G、H分别为各边的中点,求四边形EFGH的形状.
解:连接AC、BD,
∵E、F、G、H分别为各边的中点,
∴EH、GF分别为△ABD与△BCD的中位线,
∴EH∥BD∥GF,EH=GF=![]() BD,
BD,
∴四边形EFGH是平行四边形,
同理可得,HG∥AC∥EF,
∵AC⊥BD,
∴HG⊥BD⊥EH,
∴四边形EFGH是矩形.






