Question

【题目】如图，∠1=75°，∠A=60°，∠B=45°，∠2=∠3，FH⊥AB于H．
（1）求证：DE∥BC；
（2）CD与AB有什么位置关系？证明你的猜想．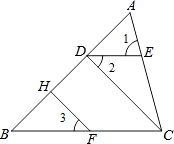

Answer 1

【答案】
（1）解：证明：∵∠A+∠B+∠ACB=180°，

∴∠ACB=180°﹣60°﹣45°=75°，

而∠1=75°，

∴∠1=∠ACB，

∴DE∥BC；

（2）解：CD⊥AB．理由如下：

∵DE∥BC，

∴∠2=∠BCD，

∵∠2=∠3，

∴∠3=∠BCD，

∴FH∥CD，

∵FH⊥AB，

∴CD⊥AB．

【解析】（1）先根据三角形内角和定理计算出∠ACB=75°，则∠1=∠ACB，然后根据同位角相等，两直线平行可判断DE∥BC；（2）由DE∥BC，根据平行线的性质得∠2=∠BCD，而∠2=∠3，所以∠3=∠BCD，则可根据内错角相等，两直线平行得FH∥CD，由于FH⊥AB，根据平行线的性质得CD⊥AB．
【考点精析】利用垂线的性质和平行线的判定与性质对题目进行判断即可得到答案，需要熟知垂线的性质：1、过一点有且只有一条直线与己知直线垂直．2、垂线段最短；由角的相等或互补（数量关系）的条件，得到两条直线平行（位置关系）这是平行线的判定；由平行线（位置关系）得到有关角相等或互补（数量关系）的结论是平行线的性质．