Question

【题目】已知：如图所示，△ABC中，∠BAC=90°，AB=AC，分别过点B、C作经过点A的直线l的垂线段BD、CE，垂足分别D、E．

（1）求证：DE=BD+CE．

（2）如果过点A的直线经过∠BAC的内部，那么上述结论还成立吗？请画出图形，直接给出你的结论（不用证明）．

Answer 1

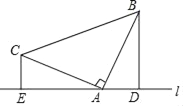
【答案】（1）见解析；（2）上述结论不成立．

【解析】试题分析：（1）由垂线的定义和角的互余关系得出 由AAS证明≌，得出对应边相等 由 即可得出结论；
（2）由垂线的定义和角的互余关系得出 由AAS证明≌，得出对应边相等由 之间的和差关系，即可得出结论．

试题解析：(1)∵∠BAC=，

∴∠BAD+∠CAE=，

∵BD⊥l，CE⊥l，

∴∠ADB=∠CEA=，

∴∠BAD+∠ABD=，

∴∠ABD=∠CAE.

在△ABD和△CAE中，

∴△ABD≌△CAE(AAS)，

∴BD=AE，AD=CE，

∵AD+AE=DE，

∴BD+CE=DE；

(2)上述结论不成立，

如图所示，BD=DE+CE.

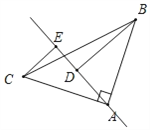
证明：∵∠BAC=，

∴∠BAD+∠CAE=，

∵BD⊥l，CE⊥l，

∴∠ADB=∠CEA=，

∴∠BAD+∠ABD=，

∴∠ABD=∠CAE.

在△ABD和△CAE中，

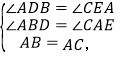
∴△ABD≌△CAE(AAS)，

∴BD=AE，AD=CE，

∵AD+DE=AE，

∴BD=DE+CE.

如图所示，CE=DE+BD，

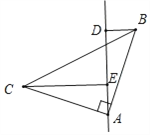
证明：证明：∵∠BAC=，

∴∠BAD+∠CAE=，

∵BD⊥l，CE⊥l，

∴∠ADB=∠CEA=，

∴∠BAD+∠ABD=，

∴∠ABD=∠CAE.

在△ABD和△CAE中，

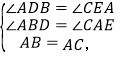
∴△ABD≌△CAE(AAS)，

∴BD=AE，AD=CE，

∵AE+DE=AD，

∴CE=DE+BD.