题目内容
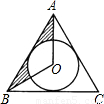
（2000•湖州）如图，已知正△ABC的边长为18，⊙O是它的内切圆，则图中阴影部分的面积为 ．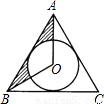
【答案】分析：要求阴影部分的面积就要明确S阴影=
S△ABC-
S⊙O，然后依面积公式计算即可．
解答：解：△ABC是正三角形，⊙O是它的内切圆，
所以△AOB的面积是正△ABC的
，扇形的面积是圆面积的
，
阴影部分的面积=
S△ABC-
S⊙O，
因为正△ABC的边长为18，
则正三角形的高为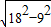
=9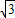
，
⊙O的半径=3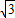
，
所以S阴影=
S△ABC-
S⊙O=
（
×18×9
-27π）=27
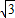-9π．
点评：本题考查了内切圆的性质及等腰三角形面积公式及圆的面积公式．
S△ABC-S⊙O，然后依面积公式计算即可．解答：解：△ABC是正三角形，⊙O是它的内切圆，
所以△AOB的面积是正△ABC的
，扇形的面积是圆面积的，阴影部分的面积=
S△ABC-S⊙O，因为正△ABC的边长为18，
则正三角形的高为
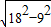=9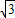，⊙O的半径=3
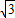，所以S阴影=
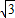S△ABC-S⊙O=（×18×9-27π）=27-9π．点评：本题考查了内切圆的性质及等腰三角形面积公式及圆的面积公式．
练习册系列答案
阅读快车系列答案
相关题目
= ．
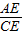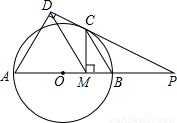
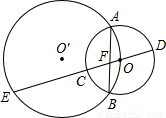
BC，CF=12，求AF的长．