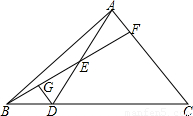
题目内容
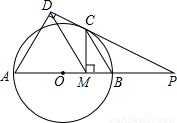
(2000•湖州)如图,已知点D是等腰直角三角形ABC的斜边BC上的一点,BC=3BD,CE⊥AD,则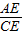 = .
= .
【答案】分析:过点D作DM⊥AC,易证∠MDA=∠ACE,因而tan∠ACE=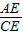 =tan∠ADM=
=tan∠ADM= .设等腰直角三角形的直角边是1,因而AC=AB=1,易证DM∥AB,△CDM∽△CBA,因而AM=
.设等腰直角三角形的直角边是1,因而AC=AB=1,易证DM∥AB,△CDM∽△CBA,因而AM= ,DM=
,DM= ,因而
,因而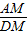 =
= ,则
,则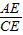 =
= .
.
解答: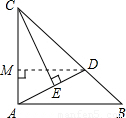 解:过点D作DM⊥AC,∵CE⊥AD,
解:过点D作DM⊥AC,∵CE⊥AD,
∴∠MDA+∠CAD=∠ACE+∠CAD=90°,
∴∠MDA=∠ACE,
∴tan∠ACE=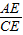 =tan∠ADM=
=tan∠ADM=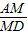 .
.
设等腰直角三角形的直角边是1,
∴AC=AB=1,
∵DM⊥AC,AB⊥AC,
∴DM∥AB,
∴△CDM∽△CBA,
而BC=3BD,
∴AM= ,DM=
,DM= ,
,
∴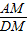 =
= ,
,
则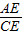 =
= .
.
故填空答案: .
.
点评:本题把求线段的比转化为相似三角形对应边成比例来求.
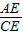 =tan∠ADM=
=tan∠ADM= .设等腰直角三角形的直角边是1,因而AC=AB=1,易证DM∥AB,△CDM∽△CBA,因而AM=
.设等腰直角三角形的直角边是1,因而AC=AB=1,易证DM∥AB,△CDM∽△CBA,因而AM= ,DM=
,DM= ,因而
,因而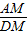 =
= ,则
,则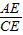 =
= .
.解答:
 解:过点D作DM⊥AC,∵CE⊥AD,
解:过点D作DM⊥AC,∵CE⊥AD,∴∠MDA+∠CAD=∠ACE+∠CAD=90°,
∴∠MDA=∠ACE,
∴tan∠ACE=
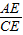 =tan∠ADM=
=tan∠ADM=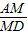 .
.设等腰直角三角形的直角边是1,
∴AC=AB=1,
∵DM⊥AC,AB⊥AC,
∴DM∥AB,
∴△CDM∽△CBA,
而BC=3BD,
∴AM=
 ,DM=
,DM= ,
,∴
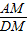 =
= ,
,则
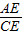 =
= .
.故填空答案:
 .
.点评:本题把求线段的比转化为相似三角形对应边成比例来求.

练习册系列答案
 53随堂测系列答案
53随堂测系列答案
相关题目
 BC,CF=12,求AF的长.
BC,CF=12,求AF的长.