题目内容
(2000•湖州)如图,已知在△ABC中,D是BC上一点,E为AD的中点,BE的延长线交AC于F,GD∥AC交BE于G.(1)求证:GE=FE;
(2)若BD=
 BC,CF=12,求AF的长.
BC,CF=12,求AF的长.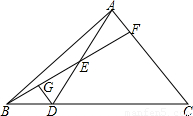
【答案】分析:(1)由于E为AD的中点,GD∥AC,由平行线的性质知,点E也是GF的中点,即GE=FE;
(2)由平行线分对应线段成比例得BD:BC=GD:CF=1:3,求得GD,由△DGE≌△AFE可得AF=GD.
解答:(1)证明:∵GD∥AC,E为AD的中点,
∴点E也是GF的中点,即GE=FE;
(2)解:∵GD∥AC,BD= BC,
BC,
∴BD:BC=GD:CF=1:3.
∵CF=12,
∴GD=4.
∵GD∥AC,
∴△DGE≌△AFE.
∴AF=GD=4.
点评:本题利用了平行线的性质,全等三角形的判定和性质求解.
(2)由平行线分对应线段成比例得BD:BC=GD:CF=1:3,求得GD,由△DGE≌△AFE可得AF=GD.
解答:(1)证明:∵GD∥AC,E为AD的中点,
∴点E也是GF的中点,即GE=FE;
(2)解:∵GD∥AC,BD=
 BC,
BC,∴BD:BC=GD:CF=1:3.
∵CF=12,
∴GD=4.
∵GD∥AC,
∴△DGE≌△AFE.
∴AF=GD=4.
点评:本题利用了平行线的性质,全等三角形的判定和性质求解.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
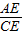 = .
= .