题目内容
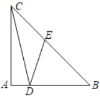
【题目】如图，
是等腰直角三角形，
，
，
，
，那么
________．
【答案】
【解析】
过点D作DF⊥BC于F，根据勾股定理即可求出BC，设
=x，根据等边对等角、三角形外角的性质和三角形的内角和定理即可求出∠DEB，再利用锐角三角函数即可求出EF和BF，最后根据BF＋EF＋CE=BC列出方程即可求出结论．
解：过点D作DF⊥BC于F
∵
是等腰直角三角形，
，
∴AB=AC=1，∠B=45°
∴BC=
，△BDF为等腰直角三角形，DF=BF
设=x
∴∠ECD=∠EDC
∴∠DEB=∠ECD＋∠EDC=2∠EDC
∴
=
（180°－∠EDC）=90°－∠EDC
∵∠DEB＋∠EDB＋∠B=180°
∴2∠EDC＋90°－∠EDC＋45°=180°
解得：∠EDC=30°
∴∠DEB=60°
∴EF=DE·cos∠DEF=x，DF=DE·sin∠DEF=
x
∴BF=DF=x
∵BF＋EF＋CE=BC
∴x＋x＋x=
解得：x=
即CE=
故答案为：．
练习册系列答案
励耘书业暑假衔接宁波出版社系列答案
相关题目
【题目】某公司计划投资
万元引进一条汽车配件流水生产线，经过调研知道该流水生产线的年产量为
件，每件总成本为
万元，每件出厂价
万元；流水生产线投产后，从第
年到第
年的维修、保养费用累计
(万元)如下表：
第 |
|
|
|
|
|
| ··· |
维修、保养费用累计 |
|
|
|
|
|
| ··· |
若上表中第年的维修、保养费用累计(万元)与的数量关系符合我们已经学过的一次函数、二次函数、反比例函数中某一个．
（1）求出关于的函数解析式；
（2）投产第几年该公司可收回万元的投资？
（3）投产多少年后，该流水线要报废(规定当年的盈利不大于维修、保养费用累计即报费)？
