题目内容
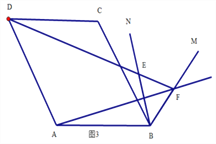
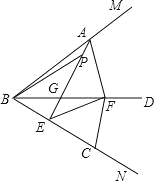
【题目】如图,射线BD是∠MBN的平分线,点A、C分别是角的两边BM、BN上两点,且AB=BC,E是线段BC上一点,线段EC的垂直平分线交射线BD于点F,连结AE交BD于点G,连结AF、EF、FC.

(1)求证:AF=EF;
(2)求证:△AGF∽△BAF;
(3)若点P是线段AG上一点,连结BP,若∠PBG=![]() ∠BAF,AB=3,AF=2,求
∠BAF,AB=3,AF=2,求![]() .
.
【答案】(1)见解析;
(2)见解析;
(3)![]() =
=![]()
【解析】
试题分析:(1)由于EF=CF,要证AF=EF,只需证FA=FC,只需证△ABF≌△CBF即可;
(2)由于∠AFG=∠BFA,要证△AGF∽△BAF,只需证∠FAE=∠ABF,易得∠FAE=∠FEA,∠ABF=∠CBF,只需证∠ABC+∠AFE=180°,只需证∠BAF+∠BEF=180°,只需证到∠BAF=∠FEC即可;
(3)由△AGF∽△BAF可得∠BAF=∠AGF,![]() =
=![]() ,易证△BGE∽△AGF,则有
,易证△BGE∽△AGF,则有![]() =
=![]() ,由条件∠PBG=
,由条件∠PBG=![]() ∠BAF可得∠PBG=
∠BAF可得∠PBG=![]() ∠AGF,由此可得∠BPG=∠PBG,即可得到BG=PG,问题得以解决.
∠AGF,由此可得∠BPG=∠PBG,即可得到BG=PG,问题得以解决.
试题解析: (1)∵BF平分∠ABC,
∴∠ABF=∠CBF.
在△ABF和△CBF中,
BA=BC, ∠ABF=∠CBF,BF=BF,
∴△ABF≌△CBF,
∴AF=CF.
∵点F在EC的垂直平分线上,
∴EF=CF,
∴AF=EF;
(2)∵△ABF≌△CBF,
∴∠BAF=∠BCF.
∵FE=FC,
∴∠FEC=∠FCE,
∴∠BAF=∠FEC.
∵∠BEF+∠FEC=180°,
∴∠BAF+∠BEF=180°.
∵∠BAF+∠ABE+∠BEF+∠AFE=360°,
∴∠ABE+∠AFE=180°.
∵FA=FE,
∴∠FAE=∠FEA.
∵∠AFE+∠FAE+∠FEA=180°,
∴∠ABE=∠FAE+∠FEA=2∠FAE.
又∵∠ABE=2∠ABF,
∴∠FAE=∠ABF.
∵∠AFG=∠BFA,
∴△AGF∽△BAF;
(3)∵△AGF∽△BAF,
∴∠AGF=∠BAF,![]() .
.
∵∠PBG=![]() ∠BAF,AB=3,AF=2,
∠BAF,AB=3,AF=2,
∴∠PBG=![]() ∠AGF,
∠AGF,![]() =
=![]() ,
,
∴∠BPG=∠PBG,![]() =
=![]() ,
,
∴PG=BG,
∴![]() .
.
∵∠GAF=∠ABF=∠EBF,∠AGF=∠BGE,
∴△BGE∽△AGF,
∴![]() =
=![]() ,
,
∴![]() =
=![]() .
.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案