Question

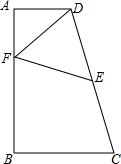
如图，在梯形ABCD中，AD∥BC，∠ABC=90°，DG⊥BC于G，BH⊥DC于H，CH=DH，点E在AB上，点F在BC上，并且EF∥DC．
（1）若AD=3，CG=2，求CD；
（2）若CF=AD+BF，求证：EF=

1

2

CD．

Answer 1

（1）连BD，如图，
∵在梯形ABCD中，AD∥BC，∠ABC=90°，DG⊥BC，
∴四边形ABGD为矩形，
∴AD=BG=3，AB=DG，
又∵BH⊥DC，CH=DH，
∴△BDC为等腰三角形，
∴BD=BG+GC=3+2=5，
在Rt△ABD中，AB=

BD2-AD2

=

52-32

=4，
∴DG=4，
在Rt△DGC中，
∴DC=

DG2+GC2

=

42+22

=2

5

．

（2）证明：∵CF=AD+BF，
∴CF=BG+BF，
∴FG+GC=BF+FG+BF，即GC=2BF，
∵EF∥DC，
∴∠BFE=∠GCD，
∴Rt△BEF∽Rt△GDC，
∴EF：DC=BF：GC=1：2，
∴EF=

1

2

DC．