题目内容
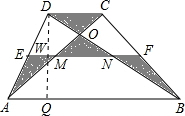
(11·贺州)如图,在梯形ABCD中,AB∥CD,AB=3CD,对角线AC、BD交
于点O,中位线EF与AC、BD分别交于M、N两点,则图中阴影部分的面积是梯形ABCD
面积的

于点O,中位线EF与AC、BD分别交于M、N两点,则图中阴影部分的面积是梯形ABCD
面积的


C
分析:首先根据梯形的中位线定理,得到EF∥CD∥AB,再根据平行线等分线段定理,得到M,N分别是AC,BD的中点;然后根据三角形的中位线定理得到CD=2EM=2NF,最后根据梯形面积求法以及三角形面积公式求出,即可求得阴影部分的面积与梯形ABCD面积的面积比.
解答:解:过点D作DQ⊥AB,交EF于一点W,
∵EF是梯形的中位线,
∴EF∥CD∥AB,DW=WQ,
∴AM=CM,BN=DN.
∴EM= CD,NF=
CD,NF= CD.
CD.
∴EM=NF,
∵AB=3CD,设CD=x,
∴AB=3x,EF=2x,
∴MN=EF-(EM+FN)=x,
∴S△AME+S△BFN= ×EM×WQ+
×EM×WQ+ ×FN×WQ=
×FN×WQ= (EM+FN)QW=
(EM+FN)QW= x?QW,
x?QW,
S梯形ABFE= (EF+AB)×WQ=
(EF+AB)×WQ=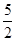 x?QW,
x?QW,
S△DOC+S△OMN= CD×DW=
CD×DW= x?QW,
x?QW,
S梯形FECD= (EF+CD)×DW=
(EF+CD)×DW=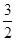 x?QW,
x?QW,
∴梯形ABCD面积=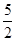 x?QW+
x?QW+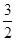 x?QW=4x?QW,
x?QW=4x?QW,
图中阴影部分的面积= x?QW+
x?QW+ x?QW=x?QW,
x?QW=x?QW,
∴图中阴影部分的面积是梯形ABCD面积的: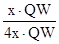 =
=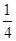 .
.
故选:C.
解答:解:过点D作DQ⊥AB,交EF于一点W,

∵EF是梯形的中位线,
∴EF∥CD∥AB,DW=WQ,
∴AM=CM,BN=DN.
∴EM=
 CD,NF=
CD,NF= CD.
CD.∴EM=NF,
∵AB=3CD,设CD=x,
∴AB=3x,EF=2x,
∴MN=EF-(EM+FN)=x,
∴S△AME+S△BFN=
 ×EM×WQ+
×EM×WQ+ ×FN×WQ=
×FN×WQ= (EM+FN)QW=
(EM+FN)QW= x?QW,
x?QW,S梯形ABFE=
 (EF+AB)×WQ=
(EF+AB)×WQ=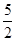 x?QW,
x?QW,S△DOC+S△OMN=
 CD×DW=
CD×DW= x?QW,
x?QW,S梯形FECD=
 (EF+CD)×DW=
(EF+CD)×DW=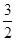 x?QW,
x?QW,∴梯形ABCD面积=
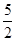 x?QW+
x?QW+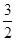 x?QW=4x?QW,
x?QW=4x?QW,图中阴影部分的面积=
 x?QW+
x?QW+ x?QW=x?QW,
x?QW=x?QW,∴图中阴影部分的面积是梯形ABCD面积的:
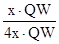 =
=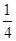 .
.故选:C.

练习册系列答案
相关题目
 ,
, ,
, ,将纸片折叠使
,将纸片折叠使 、
、 两点重合,
两点重合,



 ,则此梯形的面积为
,则此梯形的面积为


