��Ŀ����
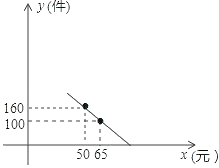
����Ŀ��ij�̳��ϰ��һ����������Ʒ������������м�¼����֪������Ʒ����Ϊÿ�� 40 Ԫ��������¼�������֣������۵����� 40 Ԫ�� 90 Ԫ֮������40 Ԫ�� 90 Ԫ��ʱ��ÿ�µ������� y�����������۵��� x��Ԫ��֮��Ĺ�ϵ�ɽ��Ƶؿ���һ�κ�������ͼ����ͼ��ʾ��
��1���� y �� x �ĺ�����ϵʽ��
��2�����̳��ϰ�ÿ�»�õ�����ΪP��Ԫ������ P �� x ֮��ĺ�����ϵʽ���������������ʱ���۵���Ϊ����Ԫ��
��3�������Ҫÿ�»�� 2400 Ԫ��������ô���۵���Ӧ��Ϊ����Ԫ��
���𰸡���1��y=��4x+360��40��x��90����2����������ʱ���۵���Ϊ 65 Ԫ��3��60 Ԫ�� 70 Ԫ
��������
��1������ͼ���ϵĵ�����꣬�ɴ���ϵ������һ�κ�������ʽ���ɵó��𰸣�
��ÿһ���������������=��������ó� p �� x �ĺ�����ϵʽΪ��p=��x��
40������4x+360����Ȼ����ݶ��κ��������ʼ��ɵõ����ۣ�
���õ� P=2400 ʱ���г�������� x ��ֵ���ɣ�
��1���� y �� x �ĺ�����ϵʽΪ��y=kx+b��k��0����
�������![]() �����
�����![]()
�� y=��4x+360��40��x��90����
��2��������ã�p �� x �ĺ�����ϵʽΪ��
p=��x��40������4x+360��=��4x2+520x��14400��
��x=��![]() =��
=��![]() =65��
=65��
����������ʱ���۵���Ϊ 65 Ԫ��
��3���� P=2400 ʱ����4x2+520x��14400=2400�� ��ã�x1 =60��x2=70��
�����۵���Ӧ��Ϊ 60 Ԫ�� 70 Ԫ��