Question

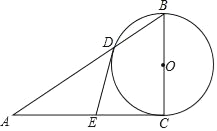
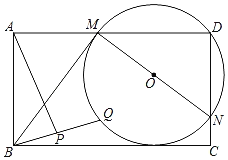
【题目】矩形ABCD的边AB＝4，边AD上有一点M，连接BM，将MB绕M点逆时针旋转90°得MN，N恰好落在CD上，过M、D、N作⊙O，⊙O与BC相切，Q为⊙O上的动点，连BQ，P为BQ中点，连AP，则AP的最小值为_____．

Answer 1

【答案】．

【解析】

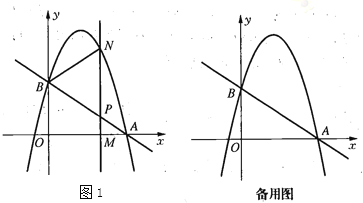
设⊙O与BC的交点为F，连接OB、OF，如图1所示．根据旋转的性质得到MN⊥BM，推出△BMN为等腰直角三角形，由全等三角形的性质得到DM=AB=4，DN=AM，设DN=2a，则AM=2a，OF=4-a，根据勾股定理即可求得⊙O半径，延长BA，使AH=AB=4，连接HQ，OH，过O作OG⊥AB于G，根据三角形中位线的定理得到AP=HQ，HQ∥AP，当HQ取最小值时，AP有最小值，当点Q在HO时，HQ的值最小，根据勾股定理可求得OH，于是可得到结论．

设⊙O与BC的交点为F，连接OB、OF，作OR⊥DC于R，如图所示．

∵△MDN为直角三角形，

∴MN为⊙O的直径，

∵将MB绕M点逆时针旋转90°得MN，

∴MN⊥BM，MB=MN，

∴△BMN为等腰直角三角形，

∵∠AMB+∠NMD=180°﹣∠BMN=90°，∠MBA+∠AMB=90°，

∴∠NMD=∠MBA，且BM=NP，∠A=∠NMD=90°，

∴△ABM≌△DMN(AAS)，

∴DM=AB=4，DN=AM，

设DN=2a，则AM=2a，OF=4﹣a，

∵OR⊥DC于R，

∴DR=RN=，

∵OR⊥DC，OF⊥BC，∠C=90°，

∴四边形ORCF为矩形，

∴，

BM=，

∵BM=MN=2OF，

∴=，

解得：，

∴，=，

∴⊙O半径为，

如图2，延长BA，使AH=AB=4，连接HQ，OH，过O作OG⊥AB于G，

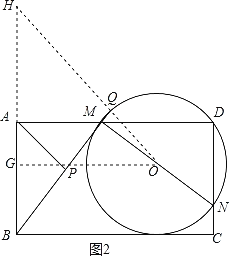
∵AB=AH，BP=PQ，

∴AP=HQ，HQ∥AP，

∴当HQ取最小值时，AP有最小值，

∴当点Q在HO时，HQ的值最小，

∵，，

∴，

∴HQ的最小值=，

∴AP的最小值为，

故答案为：．