��Ŀ����
����Ŀ�����꼶��1�����ȫ��ͬѧ�����Լ�����Ȥ���òμ�������ѧ�����ţ�ÿ��ѧ������μ���ֻ�μ�һ������Ϊ���˽�ѧ���μ����ŵ������ѧ����Ըð�μӸ������ŵ�����������ͳ�ƣ����Ƴ�����ͼ������������ͳ��ͼ����֪�μӡ������硱��ѧ����10�ˣ������������⣺ 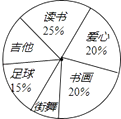
��1���ð��ѧ�����������ð�μӡ������硱������Ϊ�������ð�μӡ������硱�롰�����硱��������ͬ�������硱��Ӧ���ε�Բ�ĽǵĶ���Ϊ��
��2��һ��ѧ���ס��ҡ����ǡ������硱��������Ա����Ҫ��������ѧ�������ѡ����ѧ���μӡ������幤����������û���״ͼ���б��ķ������ǡ��ѡ�м��ҵĸ��ʣ�
���𰸡�
��1��40��8��36��
��2���⣺����״ͼ���£�
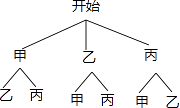
����8�ֵȿ��ܵĽ����������ǡ��ѡ�м��ҵ������2�֣�
����P��ѡ�м��ң�= ![]() =
= ![]()
���������⣺��1����Ϊ�μӡ������硱��ѧ����10�ˣ���������ͳ��ͼ�У���ռ����Ϊ25%�� ���Ըð��ѧ������10��25%=40���ˣ���
�ð�μӡ������硱������=40��20%=8��������
�μӡ������硱��ѧ����ȫ��ѧ������ռ��Ϊ ![]() ��1��25%��15%��20%��20%��=10%��
��1��25%��15%��20%��20%��=10%��
���ԡ������硱��Ӧ���ε�Բ�ĽǵĶ���Ϊ��360���10%=36�㣻
�ʴ�Ϊ40��8��36�㣻
��1�����òμӡ������硱��ѧ����������ռ�����ɼ���������ѧ������������ѧ���������ԡ������硱��ռ�İٷֱȵõ��ð�μӡ������硱��������Ȼ�������ð�μӡ������硱�İٷֱȣ��ô˰ٷֱȳ���360�ȼ��ɵõ��������硱��Ӧ���ε�Բ�ĽǵĶ�������3������״ͼչʾ����8�ֵȿ��ܵĽ���������ҳ�ǡ��ѡ�м��ҵĽ������Ȼ����ݸ��ʹ�ʽ��⣮

 �¿α�ͬ��ѵ��ϵ�д�
�¿α�ͬ��ѵ��ϵ�д� һ����ʦ����Ӧ����������һ��ȫϵ�д�
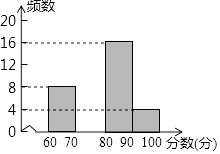
һ����ʦ����Ӧ����������һ��ȫϵ�д�����Ŀ��Ϊ���ȫ�С���ֹ���սոѡ�������ijѧУ�����ˡ���ֹ���սոѣ�������������������Ϊ������ݽ�������������ί����������ͬѧ�ijɼ��������������²�������Ƶ���ֲ�����Ƶ���ֲ�ֱ��ͼ��
�����Σ�����Ϊx�֣� | Ƶ�� | �ٷֱ� |
60��x��70 | 8 | 20% |
70��x��80 | a | 30% |
80��x��90 | 16 | b% |
90��x��100 | 4 | 10% |
�����ͼ���ṩ����Ϣ������������⣺
��1�����е�a= �� b=���벹ȫƵ���ֲ�ֱ��ͼ��
��2����������ͳ��ͼ�������ɼ��ֲ�������������70��x��80��Ӧ���ε�Բ�ĽǵĶ����Ƕ��٣�