题目内容
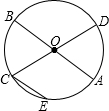如图，已知：AB和CD为⊙O的两条直径，弦CE∥AB，弧CE的度数为40°，则∠BOC=________度．
70
分析：利用平行线的性质和等腰三角形的性质即可求出．
解答：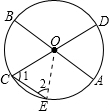
解：∵AB和CD为⊙O的两条直径，弧CE的度数为40°，
∴连接OE，则OE=OC，
∠COE=40°，
故∠1=∠2=
（180°-∠COE）=（180°-40°）=70°，
∵弦CE∥AB，
∴∠BOC=∠1=70°．
故填70°．
点评：本题考查的是平行线的性质，等腰三角形的性质及三角形内角和定理，比较简单．
分析：利用平行线的性质和等腰三角形的性质即可求出．
解答：
解：∵AB和CD为⊙O的两条直径，弧CE的度数为40°，∴连接OE，则OE=OC，
∠COE=40°，
故∠1=∠2=
（180°-∠COE）=（180°-40°）=70°，∵弦CE∥AB，
∴∠BOC=∠1=70°．
故填70°．
点评：本题考查的是平行线的性质，等腰三角形的性质及三角形内角和定理，比较简单．
练习册系列答案
相关题目
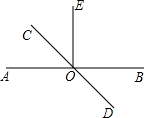（2013•奉贤区二模）如图，已知直线AB和CD相交于点O，OE⊥AB，∠AOD=128°，则∠COE的度数是
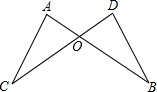如图，已知线段AB和CD相交于点O，线段OA=OD，OC=OB，求证：△OAC≌△ODB．
如图，已知线段AB和CD的公共部分BD=
如图，已知直线AB和CD相交于O点，∠COE=90°，OF平分∠AOE，∠COF=34°，求∠AOC的度数．