题目内容
【题目】已知AD∥BC,AB∥CD,E为射线BC上一点,AE平分∠BAD.
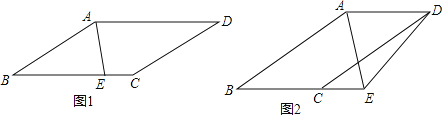
(1)如图1,当点E在线段BC上时,求证:∠BAE=∠BEA.
(2)如图2,当点E在线段BC延长线上时,连接DE,若∠ADE=3∠CDE,∠AED=60°.
①求证∠ABC=∠ADC;
②求∠CED的度数.
【答案】(1)证明见解析;(2)①证明见解析;②∠CED=135°.
【解析】
试题(1)根据平行线的性质求出∠DAE=∠BEA,由AE平分∠BAD得∠BAE=∠DAE,从而得出结论.
(2)①AD∥BC,AB∥CD即可得出结论;
②由根据∠ADE=3∠CDE设∠CDE=x°,∠ADE=3x°,∠ADC=2x°,根据平行线的性质得出方程90-x+60+3x=180,求出x即可.
试题解析:(1)证明:∵AD∥BC,
∴∠DAE=∠BEA,
∵AE平分∠BAD,
∴∠DAE=∠BAE,
∴∠BAE=∠BEA;
(2)①∵AD∥BC
∴∠ADC=∠DCE;
∵AB∥CD
∴∠ABC=∠DCE;
∴∠ABC=∠ADC;
②∵∠ADE=3∠CDE,设∠CDE=x°,
∴∠ADE=3x°,∠ADC=2x°,
∵AB∥CD,
∴∠BAD+∠ADC=180°,
∴∠DAB=180°-2x°,
由(1)可知:∠DAE=∠BAE=∠BEA=90°-x°,
∵AD∥BC,
∴∠BED+∠ADE=180°,
∵∠AED=60°,
即90-x+60+3x=180,
∴∠CDE=x°=15°,∠ADE=45°,
∵AD∥BC,
∴∠CED=180°-∠ADE=135°.

 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案【题目】代数式ax2+bx+c(a≠0,a,b,c是常数)中,x与ax2+bx+c的对应值如下表:
x | ﹣1 | ﹣ | 0 |
| 1 |
| 2 |
| 3 |
ax2+bx+c | ﹣2 | ﹣ | 1 |
| 2 |
| 1 | ﹣ | ﹣2 |
请判断一元二次方程ax2+bx+c=0(a≠0,a,b,c是常数)的两个根x1 , x2的取值范围是下列选项中的( )
A.﹣ ![]() <x1<0,
<x1<0, ![]() <x2<2
<x2<2
B.﹣1<x1<﹣ ![]() ,2<x2<
,2<x2< ![]()
C.﹣ ![]() <x1<0,2<x2<
<x1<0,2<x2< ![]()
D.﹣1<x1<﹣ ![]() ,
, ![]() <x2<2
<x2<2