Question

【题目】已知∠MON=51°，点P在∠MON的内部，点D是边ON上任意一点，点C是边OM上任意一点，连接PD、PC，当△PCD的周长最小时，∠CPD的度数为_______．

Answer 1

【答案】78°

【解析】

先找到当△PCD的周长最小时的情况，即线段AB的长度，则∠PDC=2∠A，∠PCD=2∠B，然后得到∠A+∠B的度数，由∠MON+∠APB=180°，代入计算，即可求出∠CPD的度数.

解：如图，过点P作关于OM、ON的对称点B、A， 连接AB，与OM、ON相交与点C、D，则此时△PCD的周长最小，为线段AB的长度；

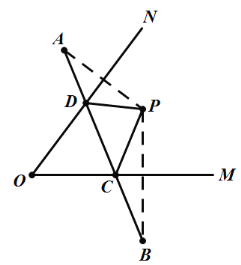
∴PD=PA，PC=BC，

∴∠A=∠APD，∠B=∠BPC，

∴∠PDC=2∠A，∠PCD=2∠B，

∴；

∵，

∴，

∴，

∴，

解得：；

故答案为：78°.