题目内容
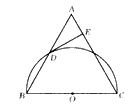
2、已知：如图所示，在等腰△ABC中，AB=AC，AD⊥BC，垂足为D，AD=3，BD=4，则图中阴影部分的面积是（ ）
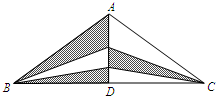
分析：观察图形，证明△BEF与△CEF全等，则阴影部分面积为正三角形面积的一半．
解答：解：∵△ABC为等边三角形，AD是BC边上的高，
∴AD垂直平分BC，
∴BF=CF，BE=CE，BD=CD，
又∵EF是公共边，
∴△BEF≌△CEF，
∴S△BEF=S△CEF，
∴阴影部分面积是△ABC面积的一半，
∵S△ABC=12，
∴阴影部分的面积是6．
故选B．
∴AD垂直平分BC，
∴BF=CF，BE=CE，BD=CD，
又∵EF是公共边，
∴△BEF≌△CEF，
∴S△BEF=S△CEF，
∴阴影部分面积是△ABC面积的一半，
∵S△ABC=12，
∴阴影部分的面积是6．
故选B．
点评：本题考查轴对称的性质，难度一般，先观察图形找到突破口，从突破口进行解题就显得比较容易，是易错题，难度适中．
练习册系列答案
相关题目
22、完成以下证明，并在括号内填写理由：
24、已知：如图所示，以△ABC的三边为边，在BC的同侧分别作等边△ABD、△BCE、△ACF．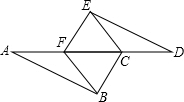
已知：如图所示，AB∥DE，AB=DE，AF=DC．
已知：如图所示，点C在线段AB上，分别以AC、BC为一边作为等边△ACM和等边△BCN，连接AN、BM．
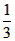CE。 