题目内容
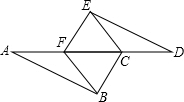 已知:如图所示,AB∥DE,AB=DE,AF=DC.
已知:如图所示,AB∥DE,AB=DE,AF=DC.(1)写出图中你认为全等的三角形(不再添加辅助线);
(2)选择你在(1)中写出的全等三角形中的任意一对进行证明.
分析:(1)根据平行线的性质确定全等三角形的对应角相等,然后根据全等三角形的判定定理SAS写出图中的全等的三角形;
(2)选择△ABF≌△DEC.根据两直线平行,内错角相等判定∠A=∠D,再由已知条件,可根据全等三角形的判定定理SAS来证明即可.
(2)选择△ABF≌△DEC.根据两直线平行,内错角相等判定∠A=∠D,再由已知条件,可根据全等三角形的判定定理SAS来证明即可.
解答:解:(1)△ABF≌△DEC,△ABC≌△DEF,△BCF≌△EFC;(2分)
(2)△ABF≌△DEC,
证明:∵AB∥DE,
∴∠A=∠D,(3分)
在△ABF和△DEC中
,(4分)
∴△ABF≌△DEC.(5分)
(2)△ABF≌△DEC,
证明:∵AB∥DE,
∴∠A=∠D,(3分)
在△ABF和△DEC中
|
∴△ABF≌△DEC.(5分)
点评:本题主要考查了全等三角形的判定、平行线的性质.本题考查三角形全等的判定方法,判定两个三角形全等的一般方法有:SSS、SAS、ASA、AAS、HL.
注意:AAA、SSA不能判定两个三角形全等,判定两个三角形全等时,必须有边的参与,若有两边一角对应相等时,角必须是两边的夹角.
注意:AAA、SSA不能判定两个三角形全等,判定两个三角形全等时,必须有边的参与,若有两边一角对应相等时,角必须是两边的夹角.

练习册系列答案
相关题目
 10、已知:如图所示,AB∥CD∥EF,BC∥AD,AC平分∠BAD,则图中与∠ACB相等的角有( )
10、已知:如图所示,AB∥CD∥EF,BC∥AD,AC平分∠BAD,则图中与∠ACB相等的角有( ) 13、已知:如图所示,AB∥CD,BC∥DE,那么∠B+∠D=
13、已知:如图所示,AB∥CD,BC∥DE,那么∠B+∠D=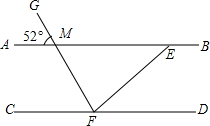 已知:如图所示,AB∥CD,EF平分∠GFD,GF交AB于M,∠GMA=52°,求∠BEF的度数.
已知:如图所示,AB∥CD,EF平分∠GFD,GF交AB于M,∠GMA=52°,求∠BEF的度数. (2013•孝南区一模)已知,如图所示,AB为⊙O的直径,AB=AC,BC交⊙O于点D,AC交于⊙O于点E,∠BAC=45°,给出以下四个结论:
(2013•孝南区一模)已知,如图所示,AB为⊙O的直径,AB=AC,BC交⊙O于点D,AC交于⊙O于点E,∠BAC=45°,给出以下四个结论: