题目内容
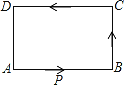
【题目】如图,在矩形ABCD中,动点P从点A开始沿A→B→C→D的路径匀速运动到点D为止,在这个过程中,下列图象可以大致表示△APD的面积S随点P的运动时间t的变化关系的是( )
A. 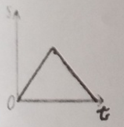 B.
B. 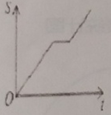 C.
C. 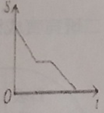 D.
D. 
【答案】D
【解析】设点P的运动速度为v,然后分点P在AB、BC、CD上三种情况根据三角形的面积公式列式表示出S与t的函数关系式,然后选择答案即可.
解:设点P的运动速度为v,
点P在AB上时,S=![]() ADAP=
ADAP=![]() vt,
vt,
点P在BC上时,S=![]() ADAB,S是定值,
ADAB,S是定值,
点P在CD上时,S=![]() (AB+BC+CD-vt)=
(AB+BC+CD-vt)=![]() (AB+BC+CD)-
(AB+BC+CD)-![]() vt,
vt,
所以,随着时间的增大,S先匀速变大至矩形的面积的一半,然后一段时间保持不变,再匀速变小至0,
纵观各选项,只有D选项图象符合.
故选D.
“点睛”本题考查了动点问题的函数图象,根据点P的位置的不同,分三段讨论求解是解题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目