题目内容
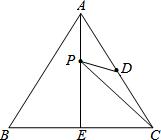等边三角形ABC的高AE=15| 3 |
考点：轴对称-最短路线问题,等边三角形的性质
专题：
分析：连接BD，由等边三角形的性质可知，点BC关于直线AE对称，所以BD的长即为PD+PC的最小值，直角三角形的性质求出BD的长即可；由相似三角形的性质得出△ADP′∽△AEC，再由相似三角形的对应边成比例即可得出DP′的长，进而可得出P′C的长．
解答：
解：连接BD，△ABC是等边三角形，D为AC的中点，
∴BD⊥AC，CD=BE=EC=15cm，∠DBC=30°，
∴BD=15
cm，即PD+PC的最小值为15
cm；
在Rt△ADP′与Rt△AEC中，
∵∠ADP′=∠AEC=90°，∠EAC=∠EAC，
∴△ADP′∽△AEC，
∴
=
，即
=
，解得DP′=5
cm，即PD=5
cm，
∴PC=BD-PD=15
-5
=10
cm．
故答案为：15
，5
，10
．
解：连接BD，△ABC是等边三角形，D为AC的中点，∴BD⊥AC，CD=BE=EC=15cm，∠DBC=30°，
∴BD=15
| 3 |
| 3 |
在Rt△ADP′与Rt△AEC中，
∵∠ADP′=∠AEC=90°，∠EAC=∠EAC，
∴△ADP′∽△AEC，
∴
| AD |
| AE |
| DP′ |
| CE |
| 15 | ||
15
|
| DP′ |
| 15 |
| 3 |
| 3 |
∴PC=BD-PD=15
| 3 |
| 3 |
| 3 |
故答案为：15
| 3 |
| 3 |
| 3 |
点评：本题考查的是轴对称-最短路线问题，熟知两点之间线段最短及等边三角形的性质是解答此题的关键．
练习册系列答案
相关题目
已知，如图在△ABC中，AC=BC，AC⊥BC，直线EF交AC于F，交AB于E，交BC的延长线于D，且CF=CD，连接AD、BF，则AD与BF之间有何关系？请证明你的结论．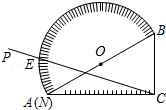
如图，量角器的直径与直角三角板ABC的斜边AB重合，其中量角器0刻度线的端点N与点A重合，射线CP从CA处出发沿顺时针方向以每秒2度的速度旋转，CP与量角器的半圆弧交于点E，第18秒，点E在量角器上对应的读数是