题目内容
如图,在直角坐标系中,⊙O的圆心O在坐标原点,直径AB=6,点P是直径AB上的一个动点(点P不与A、B两点重合),过点P的直线PQ的解析式为y=x+m,当直线PQ交y轴于Q,交⊙O于C、D两点时,过点C作CE垂直于x轴交⊙O于点E,过点E作 EG垂直于y轴,垂足为G,过点C作CF垂直于y轴,垂足为F,连接DE.
EG垂直于y轴,垂足为G,过点C作CF垂直于y轴,垂足为F,连接DE.(1)点P在运动过程中,∠CPB=
(2)当m=2时,试求矩形CEGF的面积;
(3)当P在运动过程中,探索PD2+PC2的值是否会发生变化?如果发生变化,请你说明理由;如果不发生变化,请你求出这个不变的值;
(4)如果点P在射线AB上运动,当△PDE的面积为3时,请你求出CD的长度.
分析:(1)利用图象与x,y轴交点坐标得出QO=PO,从而得出∠CPB的度数即可;
(2)利用勾股定理求出CE,OH的长度,求出矩形CEGF的面积即可;
(3)根据PC2+PD2=(CM+PM)2+(DM-PM)2,得出即可;
(4)分别从当点P在直径AB上时,以及当点P在线段AB的延长线上时得出CD与CM的长度关系,进而求出即可.
(2)利用勾股定理求出CE,OH的长度,求出矩形CEGF的面积即可;
(3)根据PC2+PD2=(CM+PM)2+(DM-PM)2,得出即可;
(4)分别从当点P在直径AB上时,以及当点P在线段AB的延长线上时得出CD与CM的长度关系,进而求出即可.
解答: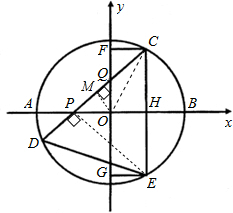 解:(1)∵过点P的直线PQ的解析式为y=x+m,
解:(1)∵过点P的直线PQ的解析式为y=x+m,
∴图象与x轴交点坐标的为:(-m,0),图象与y轴交点坐标的为:(0,m),
∴QO=PO,∠POQ=90°,
∴∠CPB=45°,
故答案为:45°;
(2)作OM⊥CD于M点,则CM=MD,
∵∠CPB=45°,CE⊥AB,
∴∠OQP=∠HCP=45°,PH=CH,
由题意得:QO=2,
∴OP=OQ=2,
∴PM=MQ=OM=
,
连接OC,则CM=
=
,
∴PC=
+
,
PH=CH=
PC=
,
∴CE=2CH=
+2,
OH=PH-OP=
-2=
,
∴S矩形CEGH=CE×OH=(
+2)×
=5;
(3)不变,
当P点在线段OA上时,由(2)得:
PC2+PD2=(CM+PM)2+(DM-PM)2,
=(CM+OM)2+(CM-OM)2,
=2(CM2+OM2),
=2OC2,
=2×32,
=18,
当P点在线段OB上时,同理可得:PC2+PD2=18,
当P点与点O重合时,显然有:PC2+PD2=18;
(4)①当点P在直径AB上时如图所示,由圆的对称性可知,
∠CPE=2∠CPB=90°,PE=PC,
∴S△PDE=
PD×PE=
PD×PC=3,
∴PD×PC=6,
即(CM-PM)(CM+PM)=6,
(CM-OM)(CM+OM)=6,
∴CM2-OM2=6,
∴CM2-(32-CM2)=6,
∴CM2=
,
∴CD=2CM=
;
②当点P在线段AB的延长线上时,如图,同理有:PD×PC=6,
即:(PM+DM)(PM-CM)=6,
(OM+CM)(OM-CM)=6,
∴OM2-CM2=6,
∴(32-CM2)-CM2=6,
∴CM2=
,
∴CD=2CM=
,
综上所述:CD为
或
.
 解:(1)∵过点P的直线PQ的解析式为y=x+m,
解:(1)∵过点P的直线PQ的解析式为y=x+m,∴图象与x轴交点坐标的为:(-m,0),图象与y轴交点坐标的为:(0,m),
∴QO=PO,∠POQ=90°,
∴∠CPB=45°,
故答案为:45°;
(2)作OM⊥CD于M点,则CM=MD,
∵∠CPB=45°,CE⊥AB,
∴∠OQP=∠HCP=45°,PH=CH,
由题意得:QO=2,
∴OP=OQ=2,
∴PM=MQ=OM=
| 2 |
连接OC,则CM=
| OC2-OM2 |
| 7 |
∴PC=
| 2 |
| 7 |
PH=CH=
| ||
| 2 |
| ||
| 2 |
∴CE=2CH=
| 14 |
OH=PH-OP=
| ||
| 2 |
| ||
| 2 |
∴S矩形CEGH=CE×OH=(
| 14 |
| ||
| 2 |
(3)不变,
当P点在线段OA上时,由(2)得:
PC2+PD2=(CM+PM)2+(DM-PM)2,
=(CM+OM)2+(CM-OM)2,
=2(CM2+OM2),
=2OC2,
=2×32,
=18,
当P点在线段OB上时,同理可得:PC2+PD2=18,
当P点与点O重合时,显然有:PC2+PD2=18;
(4)①当点P在直径AB上时如图所示,由圆的对称性可知,
∠CPE=2∠CPB=90°,PE=PC,
∴S△PDE=
| 1 |
| 2 |
| 1 |
| 2 |
∴PD×PC=6,
即(CM-PM)(CM+PM)=6,
(CM-OM)(CM+OM)=6,
∴CM2-OM2=6,
∴CM2-(32-CM2)=6,

∴CM2=
| 15 |
| 2 |
∴CD=2CM=
| 30 |
②当点P在线段AB的延长线上时,如图,同理有:PD×PC=6,
即:(PM+DM)(PM-CM)=6,
(OM+CM)(OM-CM)=6,
∴OM2-CM2=6,
∴(32-CM2)-CM2=6,
∴CM2=
| 3 |
| 2 |
∴CD=2CM=
| 6 |
综上所述:CD为
| 30 |
| 6 |
点评:此题主要考查了三角形的面积以及平方差公式应用以及一次函数的综合应用,要注意的是(4)中,要根据P点的不同位置进行分类求解.

练习册系列答案
 开心蛙状元作业系列答案
开心蛙状元作业系列答案 课时掌控随堂练习系列答案
课时掌控随堂练习系列答案 一课一练一本通系列答案
一课一练一本通系列答案
相关题目

 如图,在直角坐标系中,点P的坐标为(3,4),将OP绕原点O逆时针旋转90°得到线段OP′.
如图,在直角坐标系中,点P的坐标为(3,4),将OP绕原点O逆时针旋转90°得到线段OP′.

 ,2).画出△ABC的两个位似图形△A1B1C1,△A2B2C2,同时满足下列两个条件:
,2).画出△ABC的两个位似图形△A1B1C1,△A2B2C2,同时满足下列两个条件: