Question

如图，⊙O的半径为1，AB是⊙O的一条弦，且AB=

3

，则弦AB所对圆周角的度数为（　　）

• A、30°
• B、60°
• C、30°或150°
• D、60°或120°

Answer 1

分析：连接OA、OB，过O作AB的垂线，通过解直角三角形，易得出∠AOB的度数；由于弦AB所对的弧有两段：一段是优弧，一段是劣弧；所以弦AB所对的圆周角也有两个，因此要分类求解．

解答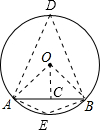：解：如图，连接OA、OB，过O作AB的垂线；
在Rt△OAC中，OA=1，AC=

3

2

；
∴∠AOC=60°，∠AOB=120°；
∴∠D=

1

2

∠AOB=60°；
∵四边形ADBE是⊙O的内接四边形，
∴∠AEB=180°-∠D=120°；
因此弦AB所对的圆周角有两个：60°或120°；
故选D．

点评：本题考查的是圆周角定理、垂径定理以及圆内接四边形的性质；注意：弦AB所对圆周角有两个，不要漏解．