题目内容
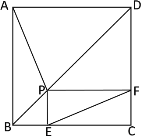
【题目】如图所示,四边形 ABCD,∠A=90°,AB=3m,BC=12m,CD=13m,DA=4m.

(1)求证:BD⊥CB;
(2)求四边形 ABCD 的面积;
【答案】(1)见解析;(2)36m2
【解析】
(1)连接BD,在直角三角形ABD中,利用勾股定理求出BD,再利用勾股定理的逆定理判断得到三角形BCD为直角三角形;
(2)四边形ABCD面积等于三角形ABD面积+三角形BCD面积,求出即可;
解:(1)连接BD,
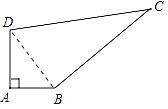
在Rt△ABD中,BD2=AB2+AD2=32+42=52,
在△CBD中,CD2=132,BC2=122,
而122+52=132,
即BC2+BD2=CD2,
∴∠DBC=90°,
∴BD⊥CB;
(2)S四边形ABCD=S△BAD+S△DBC=![]() ADAB+
ADAB+![]() DBBC=
DBBC=![]() ×4×3+
×4×3+![]() ×12×5=36m2;
×12×5=36m2;

练习册系列答案
相关题目
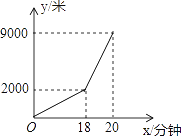
【题目】2016年10月17日7时30分,我国神舟十一号载人飞船在酒泉卫星发射中心发射升空,10月19日凌晨,神舟十一号飞船与天宫二号自动交会对接成功,32天后成功返回地面.这是中国人民的骄傲和自豪,受此鼓舞,某中学兴趣小组的同学们制作并发射了一枚小火箭,火箭发射台离地面的高度为2米,火箭离地面的高度![]() (米)与时间
(米)与时间![]() (秒)的关系如下表:
(秒)的关系如下表:
时间 | 高度 |
1 | 2+2 |
2 | 2+4 |
3 | 2+6 |
4 | 2+8 |
… | … |
(1)火箭发射10秒末离地面的高度为__________米;
(2)请你根据表中的数据写出火箭离地面的高度![]() 与时间
与时间![]() 的关系式:__________(用含
的关系式:__________(用含![]() 的式子表示
的式子表示![]() )
)
(3)利用公式求出当![]() 秒时,火箭离地面的高度.
秒时,火箭离地面的高度.