题目内容
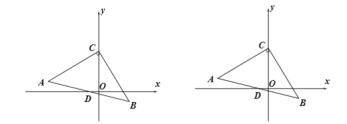
【题目】如图,已知:在坐标平面内,等腰直角![]() 中,
中,![]() ,
,![]() ,点
,点![]() 的坐标为
的坐标为![]() ,点
,点![]() 的坐标为
的坐标为![]() ,
,![]() 交
交![]() 轴于点
轴于点![]() .
.
(1)求点![]() 的坐标;
的坐标;
(2)求点![]() 的坐标;
的坐标;
(3)如图,点![]() 在
在![]() 轴上,当
轴上,当![]() 的周长最小时,求出点
的周长最小时,求出点![]() 的坐标;
的坐标;
(4)在直线![]() 上有点
上有点![]() ,在
,在![]() 轴上有点
轴上有点![]() ,求出
,求出![]() 的最小值.
的最小值.
【答案】(1)点![]() 的坐标为
的坐标为![]() ;(2)点
;(2)点![]() 的坐标为
的坐标为![]() ;(3)点
;(3)点![]() 的坐标为
的坐标为![]() ;(4)最小值为9.
;(4)最小值为9.
【解析】
(1)过C作直线EF∥x轴,分别过点A、B作直线EF的垂线,垂足分别为E、F,证明ΔACE≌ΔCBF,得到CF=AE,BF=CE,即可得到结论;
(2)分别过点A、B作x轴的垂线,垂足分别为G、H易证ΔAGD≌ΔBHD,得到GD=HD.由G(-3,0),H(1,0),即可得到结论;
(3)作点A(-5,1)关于轴的对称点A' (-5,-1),连接AP,A' P,A' C.过A' 作A' R⊥y轴于R,则AP=A' P,根据ΔACP的周长=AC+AP+CP=AC+A'P+CP≥AC+A'C.根据△A'RC和△COP都是等腰直角三角形,得到PO=CO=4,从而得到结论.
(4)作点B关于直线AC的对称点B'.过B'作B'R⊥y轴于R,过B作BT⊥y轴于T.可证明△B'RC≌△BTC,根据全等三角形对应边相等可B'的坐标.过点B'作x轴的垂线交直线AC于点M,交x轴于点N,则BM+MN=B'M+MN.根据“垂线段最短”可得它的最小值即线段B'N的长.即可得到结论.
(1)如图,过C作直线EF∥x轴,分别过点A、B作直线EF的垂线,垂足分别为E、F,
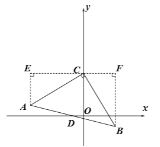
∴∠E=∠F=90°,
∴∠EAC+∠ECA=90°.
∵∠ACB=90°,
∴∠BCF+∠ECA=90°,
∴∠BCF=∠EAC.
又∵AC=BC,
∴ΔACE≌ΔCBF,
∴CF=AE,BF=CE.
∵点A(-5,1),点C(0,4),
∴CF=AE=3,BF=CE=5,且5-4=1,
∴点B的坐标为(3,-1);
(2)如图,分别过点A、B作x轴的垂线,垂足分别为G、H,
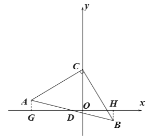
∴∠AGD=∠BHD=90°.
又∵∠ADG=∠BDH,AG=BH=1,
∴ΔAGD≌ΔBHD,
∴GD=HD.
∵G(-3,0),H(1,0),
∴GH=4,
∴GD=HD=2,
∴OD=OG-GD=3-2=1,
∴点D的坐标为(-1,0);
(3)作点A(-5,1)关于轴的对称点A' (-5,-1),连接AP,A' P,A' C.过A' 作A' R⊥y轴于R.
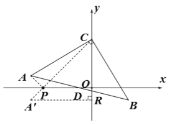
则AP=A' P,
∴ΔACP的周长=AC+AP+CP=AC+A'P+CP≥AC+A'C.
∵A'R=5,CR=CO+OR=4+1=5,
∴A'R=CR,
∴△A'RC是等腰直角三角形,
∴∠CA'R=45°.
∵A'R∥x轴,
∴∠CPO=∠CA'R=45°,
∴△COP是等腰直角三角形,
∴PO=CO=4,
∴点P的坐标为(-4,0).
(4)如图,作点B(3,-1)关于直线AC的对称点B'.过B'作B'R⊥y轴于R,过B作BT⊥y轴于T.
∵BC=B'C,∠B'RC=∠BTC=90°,∠B'CR=∠BCT,
∴△B'RC≌△BTC,
∴B'R=BT=3,CR=CT=CO+OT=4+1=5,
∴OR=OC+CR=4+5=9,
∴B'(-3,9).
过点B'作x轴的垂线交直线AC于点M,交x轴于点N,则BM+MN=B'M+MN.
根据“垂线段最短”可得它的最小值即线段B'N的长.
故BM+MN的最小值为9.

 新课标快乐提优暑假作业陕西旅游出版社系列答案
新课标快乐提优暑假作业陕西旅游出版社系列答案 暑假衔接培优教材浙江工商大学出版社系列答案
暑假衔接培优教材浙江工商大学出版社系列答案