题目内容
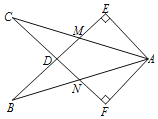
【题目】在△ABC中,AB=AC,∠BAC=120°,AD⊥BC,垂足为G,且AD=AB,∠EDF=60°,其两边分别交边AB,AC于点E,F.

(1)连接BD,求证:△ABD是等边三角形;
(2)试猜想:线段AE、AF与AD之间有怎样的数量关系?并给以证明.
【答案】(1)详见解析;(2)AE+AF=AD.证明见解析.
【解析】
(1)连接BD由等腰三角形的性质和已知条件得出∠BAD=∠DAC=![]() ,再由AD=AB,即可得出结论;
,再由AD=AB,即可得出结论;
(2)由△ABD是等边三角形,得出BD=AD,∠ABD=∠ADB=60°,证出∠BDE=∠ADF,由ASA证明△BDE≌△ADF,得出AF=BE,即可求解.
(1)证明:连接BD,
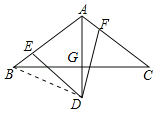
∵AB=AC,AD⊥BC,
∴∠BAD=∠DAC=![]() ∠BAC,
∠BAC,
∵∠BAC=120°,
∴![]() ,
,
∵AD=AB,
∴△ABD是等边三角形;
(2)猜想:AE+AF=AD,
理由如下:∵△ABD是等边三角形,
∴∠ABD=∠ADB=60°,AB=BD=AD
∵∠EDF=60°,
∴∠BDE=∠ADF,
在△BDE与△ADF中,
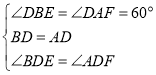
∴△BDE≌△ADF(ASA),
∴AF=BE,
∴AB=BE+AE=AF+AE=AD

练习册系列答案
相关题目
【题目】某校组织“大手拉小手,义卖献爱心”活动,计划购买黑白两种颜色的文化衫进行手绘设计后出售,并将所获利润全部捐给山区困难孩子.已知该学校从批发市场花4800元购买了 黑白两种颜色的文化衫200件,每件文化衫的批发价及手绘后的零售价如表:
批发价(元) | 零售价(元) | |
黑 色 文化衫 | 25 | 45 |
白 色 文 化 衫 | 20 | 35 |
(1)学校购进黑.白文化衫各几件?
(2)通过手绘设计后全部售出,求该校这次义卖活动所获利润.