题目内容
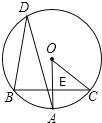
【题目】如图,已知Rt△ABC中,∠C=90°,AD是∠BAC的角平分线.
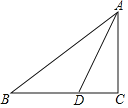
(1)请尺规作图:作⊙O,使圆心O在AB上,且AD为⊙O的一条弦.(不写作法,保留作图痕迹);
(2)判断直线BC与所作⊙O的位置关系,并说明理由.
【答案】(1)见解析;(2)直线BC与所作⊙O相切,理由见解析
【解析】
(1)作AD的垂直平分线交AB于点O,以OA为半径画圆即可;
(2)连接OD,通过等边对等角和角平分线的定义可得出∠CAD=∠ODA,从而有OD∥AC,∠ODB=∠C=90°所以BC为⊙O的切线
(1)如图,⊙O为所作;
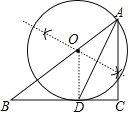
(2)直线BC与所作⊙O相切.
理由如下:连接OD,如图,
∵OA=OD,
∴∠OAD=∠ODA,
∵AD平分∠BAC,
∴∠OAD=∠CAD,
∴∠CAD=∠ODA,
∴OD∥AC,
∵∠C=90°,
∴∠ODB=90°,
∴OD⊥BC,
∴BC为⊙O的切线.

【题目】某台机床生产铸件产品,按照生产标准,铸件产品评定等级、整改费用规定如下:
重量 (单位: | 评定等级 | 整改费用 (单位:元/件) |
| 特优品 | |
| 优等品 | |
| 合格品 | |
| 不合格品 | 50 |
| 不合格品 | 30 |
注:在统计优等品个数时,将特优品计算在内;在统计合格品个数时,将优等品(含特优品)计算在内.
现该机床生产20件产品,测量其重量,得到如下统计表:
重量 (单位: |
| 29.8 | 29.9 | 30.0 | 30.1 | 30.2 |
|
件数 | 2 | 3 | 4 |
| 3 | 1 |
|
对照生产标准,发现这批铸件产品的合格率为![]() .
.
(1)求![]() 与
与![]() 的值;
的值;
(2)根据客户要求,这批铸件产品的合格率不得低于![]() .现决定从不合格产品中随机抽取两件进行整改,求整改费用最低的概率.
.现决定从不合格产品中随机抽取两件进行整改,求整改费用最低的概率.
【题目】某生产商存有1200千克![]() 产品,生产成本为150元/千克,售价为400元千克.因市场变化,准备低价一次性处理掉部分存货,所得货款全部用来生产
产品,生产成本为150元/千克,售价为400元千克.因市场变化,准备低价一次性处理掉部分存货,所得货款全部用来生产![]() 产品,
产品,![]() 产品售价为200元/千克.经市场调研发现,
产品售价为200元/千克.经市场调研发现,![]() 产品存货的处理价格
产品存货的处理价格![]() (元/千克)与处理数量
(元/千克)与处理数量![]() (千克)满足一次函数关系(
(千克)满足一次函数关系(![]() ),且得到表中数据.
),且得到表中数据.
|
|
200 | 350 |
400 | 300 |
(1)请求出处理价格![]() (元千克)与处理数量
(元千克)与处理数量![]() (千克)之间的函数关系;
(千克)之间的函数关系;
(2)若![]() 产品生产成本为100元千克,
产品生产成本为100元千克,![]() 产品处理数量为多少千克时,生产
产品处理数量为多少千克时,生产![]() 产品数量最多,最多是多少?
产品数量最多,最多是多少?
(3)由于改进技术,![]() 产品的生产成本降低到了
产品的生产成本降低到了![]() 元/千克,设全部产品全部售出,所得总利润为
元/千克,设全部产品全部售出,所得总利润为![]() (元),若
(元),若![]() 时,满足
时,满足![]() 随
随![]() 的增大而减小,求
的增大而减小,求![]() 的取值范围.
的取值范围.