题目内容
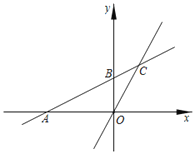
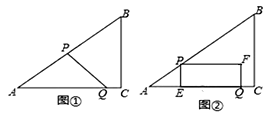
【题目】如图①,在Rt△ABC中,∠C=90°,AB=10,BC=6,点P从点A出发,沿折线AB﹣BC向终点C运动,在AB上以每秒5个单位长度的速度运动,在BC上以每秒3个单位长度的速度运动,点Q从点C出发,沿CA方向以每秒![]() 个单位长度的速度运动,P,Q两点同时出发,当点P停止时,点Q也随之停止.设点P运动的时间为t秒.
个单位长度的速度运动,P,Q两点同时出发,当点P停止时,点Q也随之停止.设点P运动的时间为t秒.
(1)求线段AQ的长;(用含t的代数式表示)
(2)连结PQ,当PQ与△ABC的一边平行时,求t的值;
(3)如图②,过点P作PE⊥AC于点E,以PE,EQ为邻边作矩形PEQF.设矩形PEQF与△ABC重叠部分图形的面积为S.直接写出点P在运动过程中S与t之间的函数关系式和自变量的取值范围.
【答案】(1)![]() ;(2)当t=1.5或t=3时,PQ与△ABC的一边平行;(3)当0≤t≤1.5时,S=-16
;(2)当t=1.5或t=3时,PQ与△ABC的一边平行;(3)当0≤t≤1.5时,S=-16![]() +24t;当1.5<t≤2时,S=
+24t;当1.5<t≤2时,S=![]() ;当2<t≤3时,S=
;当2<t≤3时,S=![]() ;当3<t≤4时,S=-4
;当3<t≤4时,S=-4![]() +16t.
+16t.
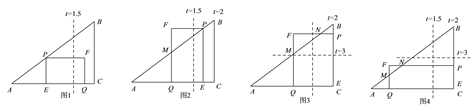
【解析】分析:(1)用勾股定理求AC,则AQ=AC-CQ;(2)用平行线分线段成比例定理列方程求t的值,要分两种情况,①当当PQ∥BC时,②当PQ∥AB时;(3)分四种情况,①当0≤t≤1.5时,②当1.5<t≤2时,③当2<t≤3时,④当3<t≤4时,根据图形得到s与t的函数关系式.
详解:(1)∵∠C=90°,∴AC=![]() =8.
=8.
∴AQ=AC-CQ=![]() .
.
(2)①当PQ∥BC时,![]() ,
,
∴![]() ,t=1.5.
,t=1.5.
②当PQ∥AB时,![]() ,
,
∴![]() ,t=3.
,t=3.
∴当t=1.5或t=3时,PQ与△ABC的一边平行.
(3)如图1,当0≤t≤1.5时,S=-16![]() +24t;
+24t;
如图2,当1.5<t≤2时,S=![]() ;
;
如图3,当2<t≤3时,S=![]() ;
;
如图4,当3<t≤4时,S=-4![]() +16t.
+16t.

练习册系列答案
 小学夺冠AB卷系列答案
小学夺冠AB卷系列答案 ABC考王全优卷系列答案
ABC考王全优卷系列答案
相关题目