题目内容
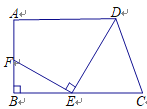
【题目】如图,在△ABC中,AB=AC,∠A=36°,BD为角平分线,DE⊥AB,垂足为E.

(1)写出图中一对全等三角形和一对相似比不为1的相似三角形;
(2)选择(1)中一对加以证明.
【答案】(1)△ADE≌△BDE,△ABC∽△BCD;(2)证明见解析.
【解析】试题分析:(1)利用相似三角形的性质以及全等三角形的性质得出符合题意的答案;
(2)利用相似三角形的判定以及全等三角形的判定方法分别得出即可.
试题解析:解:(1)△ADE≌△BDE,△ABC∽△BCD;
(2)证明:∵AB=AC,∠A=36°,
∴∠ABC=∠C=72°,
∵BD为角平分线,
∴∠ABD=![]() ∠ABC=36°=∠A,
∠ABC=36°=∠A,
在△ADE和△BDE中
∵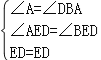 ,
,
∴△ADE≌△BDE(AAS);
证明:∵AB=AC,∠A=36°,
∴∠ABC=∠C=72°,
∵BD为角平分线,
∴∠DBC=![]() ∠ABC=36°=∠A,
∠ABC=36°=∠A,
∵∠C=∠C,
∴△ABC∽△BCD.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目