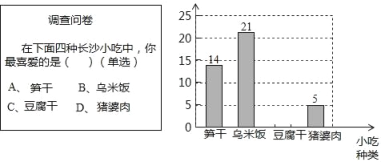
题目内容
【题目】在△ABC中,AB=AC,BC=12,已知圆O是△ABC的外接圆,且半径为10,则BC边上的高为_____.
【答案】2或18
【解析】
分点A在优弧和劣弧上两种情况,当A在优弧上时,过A作AD⊥BC于点D,则可知O在AD上,连接BD,在Rt△BOD中可求得OD=5,可知AD=8+10,当点A在劣弧上时可知AD=OA-AD=2.
如图1,当点A在优弧上时,过A作AD⊥BC于点D,
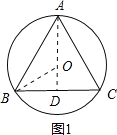
∵AB=AC,
∴BD=CD=6,且圆心O在AD上,
连接OB,则OB=OA=10,
在Rt△BOD中,由勾股定理可求得OD=8,
∴AD=AO+OD=10+8=18;
如图2,当点A在劣弧上时,过A作AD⊥BC于点D,
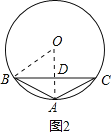
∵AB=AC,
∴BD=CD=6,且圆心O在AD上,
连接OB,则OB=OA=10,
在Rt△BOD中,由勾股定理可求得OD=8,
∴AD=AOOD=108=2;
综上可知△ABC的BC边上的高为2或18,
故答案为:2或18.

练习册系列答案
相关题目