��Ŀ����
����Ŀ����ͼ����ƽ��ֱ������ϵ�У���A����Ϊ��6��0������B��y����������ϣ���S��AOB=24��
��1�����B���ꣻ
��2������P��B������y�Ḻ�����˶����ٶ�ÿ��2����λ���˶�ʱ��t�룬��AOP�����ΪS����S��t�Ĺ�ϵʽ����ֱ��д��t��ȡֵ��Χ��
��3���ڣ�2���������£���S��AOP��S��ABP=1��3����S��AOP+S��ABP=S��AOB �� ���߶�AB�Ĵ�ֱƽ�������Ƿ���ڵ�Q��ʹ�á�AOQ��������BPQ�������ȣ������ڣ����Q�����ꣻ�������ڣ���˵�����ɣ�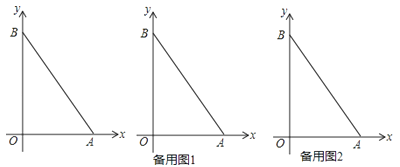
���𰸡��⣺��1���ߵ�A����Ϊ��6��0����
��OA=6��
��S��AOB=![]() ��OA��OB=24��
��OA��OB=24��
��OB=8��
���B������0��8����
��2����0��t��4ʱ��S=![]() ����8��2t����6=24��6t��
����8��2t����6=24��6t��
��t��4ʱ��S=![]() ����2t��8����6=6t��24��
����2t��8����6=6t��24��
��3����S��AOP+S��ABP=S��AOB ��
���P���߶�OB�ϣ�
��S��AOP��S��ABP=1��3��
��OP��BP=1��3��
�֡�OB=8��
��OP=2��BP=6��
�߶�AB�Ĵ�ֱƽ�����Ͻ�OB��E����AB��F��
��OB=8��OA=6��
��AB=![]() =10��
=10��
���F��������3��4����
��EF��AB����AOB=90�㣬
���BEF�ס�BAO��
��![]() =
=![]() ����
����![]() =
=![]() ��
��
��ã�BE=![]() ��
��
��OE=8��![]() =
=![]() ��
��
���E��������0��![]() ����
����
��ֱ��EF�Ľ���ʽΪy=kx+b��
��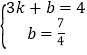 ��
��
��ã�k=![]() ��b=
��b=![]() ��
��
��ֱ��EF�Ľ���ʽΪy=![]() x+
x+![]() ��
��
�ߡ�AOQ��������BPQ�������ȣ���OA=BP��
��x=y����x=��y��
��x=yʱ��x=![]() x+
x+![]() ����ã�x=7��
����ã�x=7��
��Q��������7��7����
��x=��yʱ����x=![]() x+
x+![]() ����ã�x=��1��
����ã�x=��1��
��Q����������1��1����
��Q��������7��7����1��1����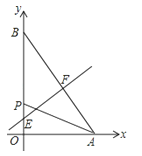
����������1�����������ε������ʽ���OB�ij����ɣ�
��2����0��t��4��t��4������������������������ʽ���㼴�ɣ�
��3����������������ε������ʽ���OP��BP�ij����������������ε����������E�����꣬�����е������ȷ����F�����꣬���ô���ϵ�������ֱ��ef�Ľ���ʽ�����ݵȵ����������������ȣ����ǵĸ�Ҳ��ȷ�x=y��x=��y����������㼴�ɣ�

 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�