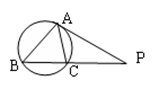
题目内容
已知在四边形ABCD中,

小题1:(1)求 的长;小题2:(2)求
的长;小题2:(2)求 的长.
的长.


小题1:(1)求
 的长;小题2:(2)求
的长;小题2:(2)求 的长.
的长.小题1:(1) 5
小题2:(2) 7
如上图所示:
过A点作AF平行且等于BC至F点,延长CF和延长AD相交于点G。
有∠FAG=120°-90°=30°,∠AFG=90°,∠AGF=60°
所以在直角三角形AFG中,有AG=6,FG=3。
所以AD=DG=6-3=3.故D为AG边的中点。连接DF,有FD=DG。
∠DFC=120°=∠BAD
又因AB=CF,DF=AD=DG
故三角形ABD与三角形CDF全等,故CD=BD=7,AB=CF
在三角形CDF中由余弦定理有:
72=32+CF2-2*3*CF*COS120°解方程有CF=5=AB
故AB长为5;CD长为7。
过A点作AF平行且等于BC至F点,延长CF和延长AD相交于点G。
有∠FAG=120°-90°=30°,∠AFG=90°,∠AGF=60°
所以在直角三角形AFG中,有AG=6,FG=3。
所以AD=DG=6-3=3.故D为AG边的中点。连接DF,有FD=DG。
∠DFC=120°=∠BAD
又因AB=CF,DF=AD=DG
故三角形ABD与三角形CDF全等,故CD=BD=7,AB=CF
在三角形CDF中由余弦定理有:
72=32+CF2-2*3*CF*COS120°解方程有CF=5=AB
故AB长为5;CD长为7。

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 ,点B为CD延长线上一点,且BD=2AD.求AB的长.
,点B为CD延长线上一点,且BD=2AD.求AB的长.
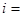 ▲ .
▲ .
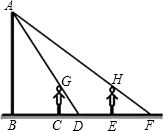
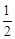 ,则河堤高BE等于( )米
,则河堤高BE等于( )米
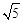



 ;
; ;
; ;
; .
.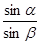 = .
= .