题目内容
下面是两位同学的一段对话:

甲:我站在此处看塔顶仰角为
乙:我站在此处看塔顶仰角为
甲:我们的身高都是1.5m
乙:我们相距20m
请你根据两位同学的对话计算塔的高度(精确到1米)是______.

甲:我站在此处看塔顶仰角为

乙:我站在此处看塔顶仰角为

甲:我们的身高都是1.5m
乙:我们相距20m
请你根据两位同学的对话计算塔的高度(精确到1米)是______.
19米
根据三角形外角和定理,可求得∠CAB=∠ACB,等角对等边,所以有AB=BC=20m.在Rt△CBD中,根据60°角的正弦值可求出CD,再加上同学自身的身高1.5米即可解答.
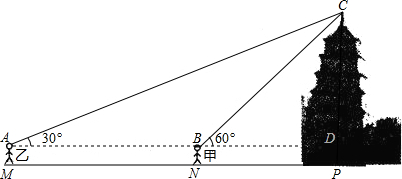
解:由题意,知:∠CAB=30°,∠CBD=60°,AB=20m,AM=BN=DP=1.5m;
在△ABC中,∠CBD=∠ACB+∠CAB,
∴∠ACB=60°-30°=30°;
∴∠ACB=∠CAB;
∴BC=AB=20m;
在Rt△CBD中,BC=20m,∠CBD=60°,
∵sin∠CBD=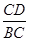 ,即sin60°=
,即sin60°=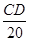 ;
;
∴CD=20sin60°=20×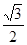 =10
=10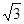 m;
m;
∴CP=CD+DP=10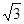 +1.5≈19m.
+1.5≈19m.
故答案为:19.本题考查了仰角的定义.此题难度适中,注意能借助仰角构造直角三角形并解直角三角形是解此题的关键,注意数形结合思想的应用.

解:由题意,知:∠CAB=30°,∠CBD=60°,AB=20m,AM=BN=DP=1.5m;
在△ABC中,∠CBD=∠ACB+∠CAB,
∴∠ACB=60°-30°=30°;
∴∠ACB=∠CAB;
∴BC=AB=20m;
在Rt△CBD中,BC=20m,∠CBD=60°,
∵sin∠CBD=
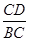 ,即sin60°=
,即sin60°=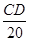 ;
;∴CD=20sin60°=20×
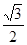 =10
=10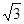 m;
m;∴CP=CD+DP=10
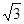 +1.5≈19m.
+1.5≈19m.故答案为:19.本题考查了仰角的定义.此题难度适中,注意能借助仰角构造直角三角形并解直角三角形是解此题的关键,注意数形结合思想的应用.

练习册系列答案
相关题目
 中,∠A=45°,
中,∠A=45°,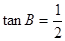 ,
,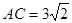 cm,求AB的长度.
cm,求AB的长度.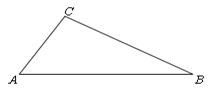
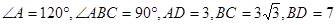

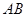 的长;小题2:(2)求
的长;小题2:(2)求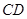 的长.
的长.
 点,并测得HB=6m.
点,并测得HB=6m.
 在图中画出形成影子的光线,并确定路灯灯泡所在的位置G;
在图中画出形成影子的光线,并确定路灯灯泡所在的位置G;