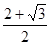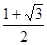题目内容
如图所示,某河堤的横断面是梯形ABCD,BC∥AD,迎水坡AB长为10米,斜坡AB的坡度i=1: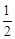 ,则河堤高BE等于( )米
,则河堤高BE等于( )米

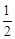 ,则河堤高BE等于( )米
,则河堤高BE等于( )米
A.4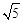 | B.2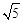 | C.4 | D.5 |
A
由已知斜坡AB的坡度i=1: ,可得到BE、AE的比例关系,进而由勾股定理求得BE、AE的长,由此得解.
,可得到BE、AE的比例关系,进而由勾股定理求得BE、AE的长,由此得解.
解:由已知斜坡AB的坡度i=1: 得:
得:
BE:AE=2:1,
设AE=x,则BE=2x,
在直角三角形AEB中,根据勾股定理得:
102=x2+(2x)2,
即5x2=100,
解得:x=2 或x=-2
或x=-2 (舍去),
(舍去),
2x=4 ,
,
即河堤高BE等于4 米.
米.
故选:A.
本题主要考查的是坡度的定义和勾股定理的应用.
 ,可得到BE、AE的比例关系,进而由勾股定理求得BE、AE的长,由此得解.
,可得到BE、AE的比例关系,进而由勾股定理求得BE、AE的长,由此得解.解:由已知斜坡AB的坡度i=1:
 得:
得:BE:AE=2:1,
设AE=x,则BE=2x,
在直角三角形AEB中,根据勾股定理得:
102=x2+(2x)2,
即5x2=100,
解得:x=2
 或x=-2
或x=-2 (舍去),
(舍去),2x=4
 ,
,即河堤高BE等于4
 米.
米.故选:A.
本题主要考查的是坡度的定义和勾股定理的应用.

练习册系列答案
相关题目
 ,则锐角
,则锐角 是
是  .
. ,并测得∠APO=59º,∠BPO=45º.
,并测得∠APO=59º,∠BPO=45º.


 的长;小题2:(2)求
的长;小题2:(2)求 的长.
的长.
 米
米 米
米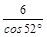 米
米 中,
中, ,
, ,
, ,那么
,那么 的长是………( )
的长是………( ) ;
; ;
; ;
; .
.

 B.
B. C.
C. D.
D.
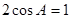 ,则锐角A的度数是( )
,则锐角A的度数是( )