题目内容
如图,在Rt△ADC中,∠C=90°,∠ADC=60°,AC= ,点B为CD延长线上一点,且BD=2AD.求AB的长.
,点B为CD延长线上一点,且BD=2AD.求AB的长.
 ,点B为CD延长线上一点,且BD=2AD.求AB的长.
,点B为CD延长线上一点,且BD=2AD.求AB的长.

考点:
分析:先根据∠ABC的正弦值求得BC的长,再根据BD=2AB,以及勾股定理求出AD的长即可.
解答:解:在Rt△ABC中,∠C=90°,∠ABC=60°,AC= ,
,
∴AB= =2,BC=1.
=2,BC=1.
∵D为CB延长线上一点,BD=2AB,
∴BD=4,CD=5.
∴AD=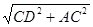 =
= .
.
点评:本题考查了解直角三角形,是基础知识要熟练掌握.
分析:先根据∠ABC的正弦值求得BC的长,再根据BD=2AB,以及勾股定理求出AD的长即可.
解答:解:在Rt△ABC中,∠C=90°,∠ABC=60°,AC=
 ,
,∴AB=
 =2,BC=1.
=2,BC=1.∵D为CB延长线上一点,BD=2AB,
∴BD=4,CD=5.
∴AD=
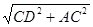 =
= .
.点评:本题考查了解直角三角形,是基础知识要熟练掌握.

练习册系列答案
 导学全程练创优训练系列答案
导学全程练创优训练系列答案
相关题目
 , 点D、E分别在AB、AC边上,DE⊥AC,DE=2,DB="9," 求DC的长.
, 点D、E分别在AB、AC边上,DE⊥AC,DE=2,DB="9," 求DC的长.

 中BC边的中点,
中BC边的中点, ,
, , AD=2
, AD=2
 ;
; = .
= .

 的长;小题2:(2)求
的长;小题2:(2)求 的长.
的长.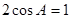 ,则锐角A的度数是( )
,则锐角A的度数是( ) 



 .
.
