Question

已知关于x的一次函数y₁=kx+1和反比例函数y2=

6

x

的图象都经过点（2，m）．
（1）求一次函数的表达式；
（2）求反比例函数的图象与一次函数的图象的两交点及坐标原点所构成的三角形的面积；
（3）观察图象，当x在什么范围内时，y₁＞y₂．

Answer 1

分析：（1）先把（2，m）代入反比例函数y₂=

6

x

求出m的值，再把点（2，m）代入y₁=kx+1即可求出k的值；
（2）根据题意画出图形，求出反比例函数的图象与一次函数的图象的两交点坐标，进而求出三角形的面积；
（3）根据图象直接观察出x的取值范围．

解答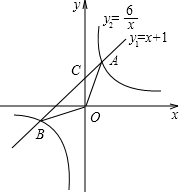：解：（1）把（2，m）代入反比例函数y₂=

6

x

得，
m=

6

2

=3；
∴点（2，3）．
把点（2，3）代入一次函数y₁=kx+1得，k=1，
∴一次函数解析式为y₁=x+1；
（2）根据题意画出图象：将y=x+1和y=

6

x

组成方程组得，

y=x+1 y= 6 x

，
解得，

x=2 y=3

，

x=-3 y=-2

，
故B（-3，-2）；A（2，3）．
当x=0时，y=1，
故C（0，1）．
∴S△AOB=S_△AOC+S_△COB=

1

2

×1×2+

1

2

×1×3=

5

2

．
（3）由图可知，-3＜x＜0或x＞2时，y₁＞y₂．

点评：本题考查了反比例函数与一次函数的交点问题，会用待定系数法以及理解函数与方程的关系是解题的关键．