��Ŀ����
����Ŀ����ͼ����֪��ABC�У�AB=AC=10cm��BC=8cm����B=��C,��DΪAB���е㣮
(1)�����P���߶�BC����3cm/s���ٶ���B����C���˶���ͬʱ����Q���߶�CA����C����A���˶���
������Q���˶��ٶ����P���˶��ٶ���ȣ�����1s��BPD���CQP�Ƿ�ȫ�ȣ���˵�����ɣ�
������Q���˶��ٶ����P���˶��ٶȲ���ȣ�����Q���˶��ٶ�Ϊʱ________cm/s�����˶��������ܹ�ʹ��BPD���CQPȫ��.(ֱ�����)
(2)����Q�Ԣ��е��˶��ٶȴӵ�C��������P��ԭ�����˶��ٶȴӵ�Bͬʱ����������ʱ���ء�ABC�����˶������ʱ���P���Q��һ���ڡ�ABC��������������?

���𰸡���1���١�BPD�ա�CQP�����ɼ���������![]() ����2������
����2������![]() s��P���Q��һ������ABC��AB��������
s��P���Q��һ������ABC��AB��������
��������
��1����ͨ��t=1��������߳���֤��ȫ�ȼ��ɣ�����Q���˶��ٶ����P���˶��ٶȲ���ȣ���BP��CQ����BP=PC=4��CQ=BD=5������ٶȼ��ɣ���2����P�͵�Q�൱��Χ�š�ABC��ʱ���˶��������⣬�ҵ��ٶȲ����·�̼��ɽ��.
�⣺��1���١�BPD�ա�CQP��
�������£�
��t=1s��
��BP=CQ=3��1=3��cm����
��AB=10cm����DΪAB���е㣬
��BD=5cm��
�֡�PC=BC-BP��BC=8cm��
��PC=8-3=5��cm����
��PC=BD��
�֡�AB=AC��
���B=��C��
�ڡ�BPD�͡�CQP��
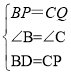
���BPD�ա�CQP��SAS����
��P��Q���ٶȲ���ȣ�
��BP��CQ��
�ߡ�BPD�ա�CQP����B=��C��
��BP=PC=4��CQ=BD=5��
���P����Q�˶���ʱ��t=![]()
��vQ=5��![]() =
=![]() cm/s��
cm/s��
�൱��Q���˶��ٶ�Ϊ![]() cm/s�ܹ�ʹ��BPD���CQPȫ�ȣ�
cm/s�ܹ�ʹ��BPD���CQPȫ�ȣ�
��2����P����ٶ�Ϊ3 cm/s����Q���˶��ٶ�Ϊ![]() cm/s��
cm/s��
Q��P�ٶȲ�Ϊ![]() -3=
-3=![]() cm/s��
cm/s��
���ϵ�ʱ��Ϊ20��![]() =
=![]() s��
s��
��P�˶�·��Ϊ![]() ��3=80cm��
��3=80cm��
��BA=AC=10cm��CB=8cm��
���ABC���ܳ�Ϊ28cm,
80��28=2������������24cm��24-8-10=6cm��
����AB���ϵ�P���Q��һ������.

 ����ʦ��Сһ����ʦ������ҵϵ�д�
����ʦ��Сһ����ʦ������ҵϵ�д� ���100�ֵ�Ԫ�Ż�������ϵ�д�
���100�ֵ�Ԫ�Ż�������ϵ�д�




