��Ŀ����
�Ķ����в��ϣ�������ѧϰ���θ�ʽʱ��ʽ��
�����壬��x��0��ʽ��
�����壬��x��0����ʽ��
+
�����壬��x��ȡֵ��Χ������������ת��Ϊ����ʽ����������������x�IJ���ʽ��
�Ľ⼯�����������ʽ���x=0������������������ѧ��������������⣺
��1��ʽ��
+
�����壬��x��ȡֵ��Χ��
��2����֪��y=
+
-3����xy��ֵ��
| x |
| -x |
| x |
| -x |
|
��1��ʽ��
| x2-1 |
| 1-x2 |
��2����֪��y=
| x-2 |
| 2-x |
��1����ʽ��
+
�����壬
��
��
���x=��1��
��2����y=
+
-3��
��
��
���x=2��
��y=-3��
��xy=2-3=
��
| x2-1 |
| 1-x2 |
��
|
���x=��1��
��2����y=
| x-2 |
| 2-x |
��
|
���x=2��
��y=-3��
��xy=2-3=
| 1 |
| 8 |

��ϰ��ϵ�д�
�����Ŀ
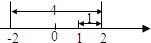 28��
28��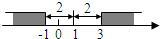 �Ķ����в��ϣ�
�Ķ����в��ϣ� �����壬��x��0��ʽ��
�����壬��x��0��ʽ�� �����壬��x��0����ʽ��
�����壬��x��0����ʽ��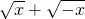 �����壬��x��ȡֵ��Χ������������ת��Ϊ����ʽ����������������x�IJ���ʽ��
�����壬��x��ȡֵ��Χ������������ת��Ϊ����ʽ����������������x�IJ���ʽ��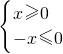 �Ľ⼯�����������ʽ���x=0������������������ѧ��������������⣺
�Ľ⼯�����������ʽ���x=0������������������ѧ��������������⣺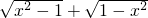 �����壬��x��ȡֵ��Χ��
�����壬��x��ȡֵ��Χ��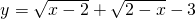 ����xy��ֵ��
����xy��ֵ��