Question

已知△ABC的三边长分别为5，5，6，则△ABC的面积为（　　）

A．12

B．15

C．24

D．25

Answer 1

分析：过点A作AD⊥BC，根据等腰三角形三线合一性质可得到BD=CD，再根据勾股定理可求得AD的长，从而根据三角形面积公式求解即可．

解答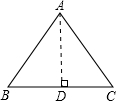：解：过点A作AD⊥BC．
∵AB=AC=5，BC=6，AD⊥BC，
∴BD=CD=3，
∴AD=4，
∴S_△ABC=

1

2

BC×AD=12．
故选：A．

点评：此题主要考查等腰三角形的性质及勾股定理的综合运用．