题目内容
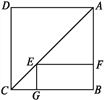
【题目】如图,点E是正方形ABCD对角线AC上一点,EF⊥AB,EG⊥BC,垂足分别为E,F,若正方形ABCD的周长是40 cm.
(1)求证:四边形BFEG是矩形;
(2)求四边形EFBG的周长;
(3)当AF的长为多少时,四边形BFEG是正方形?
【答案】(1)见解析;(2)20cm(3)当AF=5 cm时,四边形BFEG是正方形.
【解析】(1)由正方形的性质可得出AB⊥BC、∠B=90°,根据EF⊥AB、EG⊥BC利用“垂直于同一条直线的两直线互相平行”,即可得出EF∥GB、EG∥BF,再结合∠B=90°,即可证出四边形BFEG是矩形;
(2)由正方形的周长可求出正方形的边长,根据正方形的性质可得出△AEF为等腰直角三角形,进而可得出AF=EF,再根据矩形的周长公式即可求出结论;
(3)由正方形的判定可知:若要四边形BFEG是正方形,只需EF=BF,结合AF=EF、AB=10cm,即可得出结论.
(1)证明:∵四边形ABCD为正方形,
∴AB⊥BC,∠B=90°.
∵EF⊥AB,EG⊥BC,
∴EF∥GB,EG∥BF.
∵∠B=90°,
∴四边形BFEG是矩形;
(2)∵正方形ABCD的周长是40cm,
∴AB=![]() =10cm.
=10cm.
∵四边形ABCD为正方形,
∴△AEF为等腰直角三角形,
∴AF=EF,
∴四边形EFBG的周长C=2(EF+BF)=2(AF+BF)=20cm.
(3)若要四边形BFEG是正方形,只需EF=BF,
∵AF=EF,AB=10cm,
∴当AF=5cm时,四边形BFEG是正方形.

 轻松暑假总复习系列答案
轻松暑假总复习系列答案【题目】某校为了选拔学生参加“汉字听写大赛”,对九年级一班、二班各10名学生进行汉字听写测试.计分采用10分制(得分均取整数),成绩达到6分或6分以上为及格,得到9分为优秀,成绩如表1所示,并制作了成绩分析表(表2).
表1
一班 | 5 | 8 | 8 | 9 | 8 | 10 | 10 | 8 | 5 | 5 |
二班 | 10 | 6 | 6 | 9 | 10 | 4 | 5 | 7 | 10 | 8 |
表2
班级 | 平均数 | 中位数 | 众数 | 方差 | 及格率 | 优秀率 |
一班 | 7.6 | 8 | 3.82 | 70% | 30% | |
二班 | b | 7.5 | 10 | 4.94 | 80% | 40% |
(1)在表2中,a= ,b= ;
(2)有人说二班的及格率、优秀率均高于一班,所以二班比一班好;但也有人认为一班成绩比二班好,请你给出坚持一班成绩好的两条理由;
(3)一班、二班获满分的中同学性别分别是1男1女、2男1女,现从这两班获满分的同学中各抽1名同学参加“汉字听写大赛”,用树状图或列表法求出恰好抽到1男1女两位同学的概率.