题目内容
【题目】如图是某工厂货物传送带的平面示意图,为提高传送过程的安全性,工厂计划改造传动带与地面的夹角,使其AB的坡角由原来的43°改为30°.已知原传送带AB长为5米.求新旧货物传送带着地点B、C之间相距多远?(结果保留整数,参考数据:sin43°≈0.68,cos43°≈0.73,tan43°≈0.93, ![]() ≈1.41,
≈1.41, ![]() ≈1.73)
≈1.73)
【答案】解:过点A作AD垂直于CB的延长线于点D.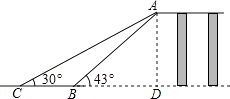
在Rt△ADB中,AB=5米,∠ABD=43°,
∵sin∠ABD= ![]() ,cos∠ABD=
,cos∠ABD= ![]() ,
,
∴AD=ABsin∠ABD=5×sin43°≈3.41米,
BD=ABcos∠ABD=5×cos43°≈3.66米.
在Rt△ADC中,
∵sin∠ACD= ![]() ,
,
AC= ![]() =6.82米,
=6.82米,
在Rt△ACD中,AC=6.82,∠ACD=30°,
∵cos∠ACD= ![]() ,
,
CD=ACcos∠ACD≈6.82×cos30°≈5.91米.
∴BC=CD﹣BD≈2米.
答:新旧货物传送带着地点B、C之间大约相距2米.
【解析】过A作BC的垂线AD.在构建的直角三角形中,首先求出两个直角三角形的公共直角边,进而在Rt△ACD中,求出AC的长.再通过解直角三角形,可求出BD、CD的长,进而可求出BC的长.
【考点精析】利用关于坡度坡角问题对题目进行判断即可得到答案,需要熟知坡面的铅直高度h和水平宽度l的比叫做坡度(坡比).用字母i表示,即i=h/l.把坡面与水平面的夹角记作A(叫做坡角),那么i=h/l=tanA.

练习册系列答案
相关题目